最近突然看到一个问题,PCA和SVD有什么关系?隐约记得自己照猫画虎实现的时候PCA的时候明明用到了SVD啊,但SVD(奇异值分解)和PCA的(特征值分解)貌似差得相当远,由此钻下去搜集了一些资料,把我的一些收获总结一下,以免以后再忘记。
PCA的简单推导
PCA有两种通俗易懂的解释,
1)是最大化投影后数据的方差(让数据更分散);地址:http://www.cnblogs.com/shixisheng/p/7107363.html
2)是最小化投影造成的损失。(下边讲的就是这个方法)
这两个思路最后都能推导出同样的结果。
下图应该是对PCA第二种解释展示得最好的一张图片了(ref:svd,pca,relation) 


def pca_01(X): covMat = np.cov(X,rowvar = 0) eigVal,eigVec = sp.linalg.eig(covMat) #do reduction with eigVal,eigVec
但因为最后用于变换的矩阵需要是去中心化后的,所以有些地方的实现是:
def pca_02(X): mean_ = np.mean(X, axis=0) X = X - mean_ covMat = np.cov(X,rowvar = 0)#实际上是否去中心化对求到的协方差矩阵并无影响,只是方便后面进行降维 eigVal,eigVec = sp.linalg.eig(covMat) #do reduction with eigVal,eigVec
使用矩阵乘法的方式:
def pca_03(X): mean_ = np.mean(X, axis=0) X = X - mean_ M,N=X.shape Sigma=np.dot(X.transpose(),X)/(M-1) eigVal,eigVec = sp.linalg.eig(Sigma) #do reduction with eigVal,eigVec
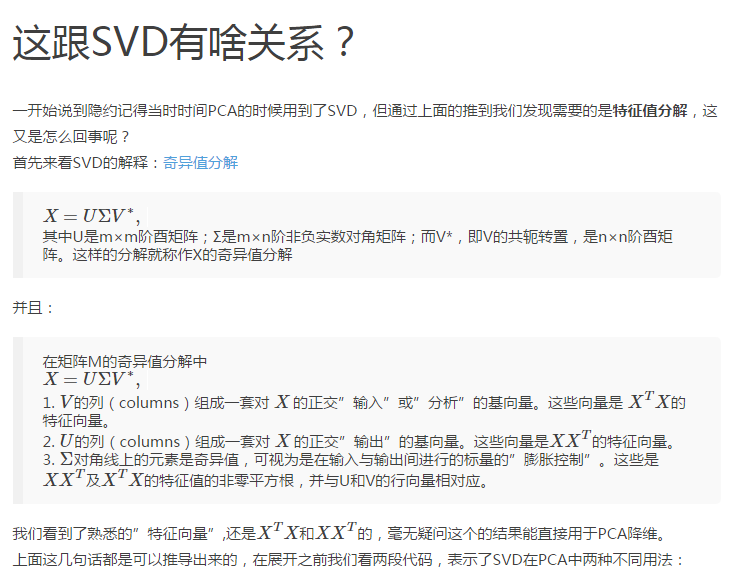
酉矩阵:n阶复方阵U的n个列向量是U空间的一个标准正交基,则U是酉矩阵(Unitary Matrix)。显然酉矩阵是正交矩阵往复数域上的推广。
def pca_04(X): mean_ = np.mean(X, axis=0) X = X - mean_ M,N=X.shape Sigma=np.dot(X.transpose(),X) #这里直接去掉/(M-1)方便和pca_05比较,对求得特征向量无影响 U,S,V = sp.linalg.svd(Sigma); eigVal,eigVec = S,U #do reduction with eigVal,eigVec
可以看到在pca_03的基础上我们把sp.linalg.eig改用了sp.linalg.svd,这涉及到:
结论1:协方差矩阵(或XTX)的奇异值分解结果和特征值分解结果一致。
def pca_05(X): mean_ = np.mean(X, axis=0) X = X - mean_ U, S, V = sp.linalg.svd(X) eigVal,eigVec = S,V #do reduction with eigVal,eigVec


PCA_04: eigVal:[ 21.60311815 8.77188185] eigVec: [[-0.88734696 -0.46110235] [-0.46110235 0.88734696]] PCA_05: eigVal:[ 4.64791546 2.96173629] eigVec: [[ 0.88734696 0.46110235] [-0.46110235 0.88734696]] #注意PCA_05结果中特征向量维度的符号,和上面不太一样,但这不影响降维的功能,每一列是一组基



转自:http://blog.csdn.net/dark_scope/article/details/53150883
