图论题笔记（一）：方格填数

题目：方格填数

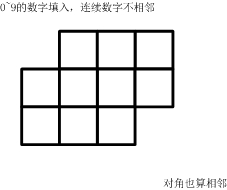
填入0~9的数字。要求：连续的两个数字不能相邻。

（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

这道题以后要翻回来看看，当前解法类似于全排列

#存储节点邻居
graph_nbr={}
#存储节点数值
graph_num={}

for row in range(3):
    for col in range(4):
        graph_nbr[(row,col)]=[]        
        graph_num[(row,col)]=None
del graph_nbr[(0,0)]
del graph_nbr[(2,3)]
del graph_num[(0,0)]
del graph_num[(2,3)]

connect=[(-1,0),(-1,-1),(-1,1),(0,-1),(0,1),(1,-1),(1,0),(1,1)]

def plus_tp(tp1,tp2):
    return (tp1[0]+tp2[0],tp1[1]+tp2[1])

#进行节点邻居的连接
for x in graph_nbr.keys():
    for ct in connect:
        result_plus=plus_tp(x,ct)
        if result_plus in graph_nbr and result_plus not in graph_nbr[x]:
            graph_nbr[x].append(result_plus)


#graph_key为所有节点
#n为搜索深度
#path为已走过路径
def dfs(graph_key,n,path,limit=10):

    #dfs结束条件
    if n==limit:
        global count
        count+=1
        print(count,graph_num)
        
    
    if n<limit:
        #从每个节点开始一次，注意以下break，不能直接理解为这个节点被永久跳过了，而是后续节点的dfs会出现新组合，任何一个数都有几率在当前节点
        for j in graph_key:
            if j not in path :
                #判断相邻的邻居是否有n-1这个数值即比当前n的小一个且相邻的数值
                has_i_prev=False
                for nbr in graph_nbr[j]:
                    if graph_num[nbr]==n-1:
                        has_i_prev=True
                        #如果有邻居已经存在前一个数字，代表这个位置不适合存放这个数字，直接跳出
                        break
                if not has_i_prev:
                    #将当前状态记下
                    graph_num[j]=n
                    path.append(j)
                    #进行dfs,并且保证已走过路径不会被遍历
                    dfs(graph_key,n+1,path)
                    #取消当前状态，假设在最深处，那么上一层还有没遍历完的节点，上一层在遍历下一个节点的时候就可以重新组合当前pop出来的节点了
                    path.pop()
                    graph_num[j]=None

mark=[]
count=0
dfs(graph_key=graph_num.keys(),n=0,path=mark)