顶点的度=顶点的入度+顶点的出度。
顶点 v 的入度是指以该顶点 v 为弧头的弧的数目;顶点 v 的出度是指以该顶点 v 为弧尾的弧的数目。
简单路径:一条路径上顶点不重复出现。
回路:第一个顶点和最后一个顶点相同的路径。
简单回路:除第一个顶点和最后一个顶点相同其余顶点都不重复的回路。
连通:在无向图中,若两个顶点之间有路径。
连通图:无向图 G 中任意两个顶点之间都是连通的。
强连通图:在有向图中,若图中任意两个顶点之间都存在从一 个顶点到另一个顶点的路径。
最小生成树:边的权值总和最小的生成树。
构造有 n 个顶点的无向连通网的最小生成树必须 满足以下三个条件:
(1)构造的最小生成树必须包括 n 个顶点;
(2)构造的最小生成树有且仅有 n-1 条边;
(3)构造的最小生成树中不存在回路。
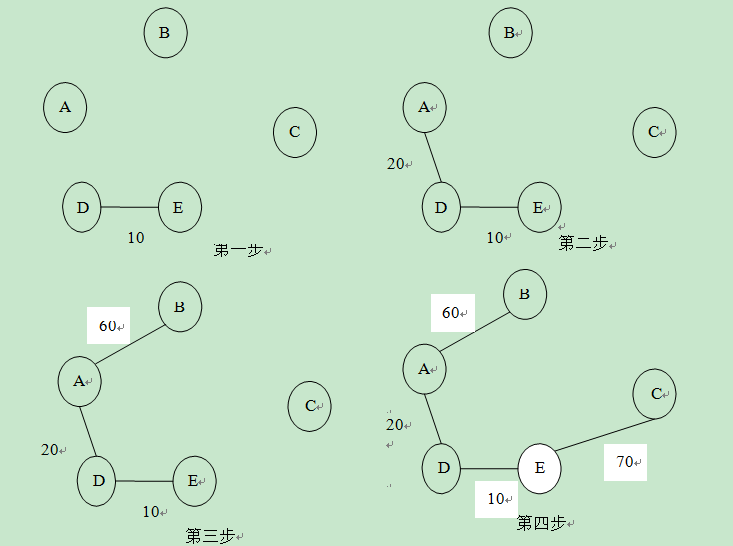
构造最小生成树的方法:普里姆(Prim);克鲁斯卡尔(Kruskal)算法。
普里姆(Prim):
假设 G=(V,E)为一无向连通网,其中,V 为网中顶点的集合,E 为网中 边的集合。设置两个新的集合 U 和 T,其中,U 为 G 的最小生成树的顶点的集 合,T 为 G 的最小生成树的边的集合。普里姆算法的思想是:令集合 U 的初值 为 U={u1}(假设构造最小生成树时从顶点 u1 开始),集合 T 的初值为 T={}。从 所有的顶点 u∈U 和顶点 v∈V-U 的带权边中选出具有最小权值的边(u,v),将顶 点 v 加入集合 U 中,将边(u,v)加入集合 T 中。如此不断地重复直到 U=V 时, 最小生成树构造完毕。此时,集合 U 中存放着最小生成树的所有顶点,集合 T中存放着最小生成树的所有边。
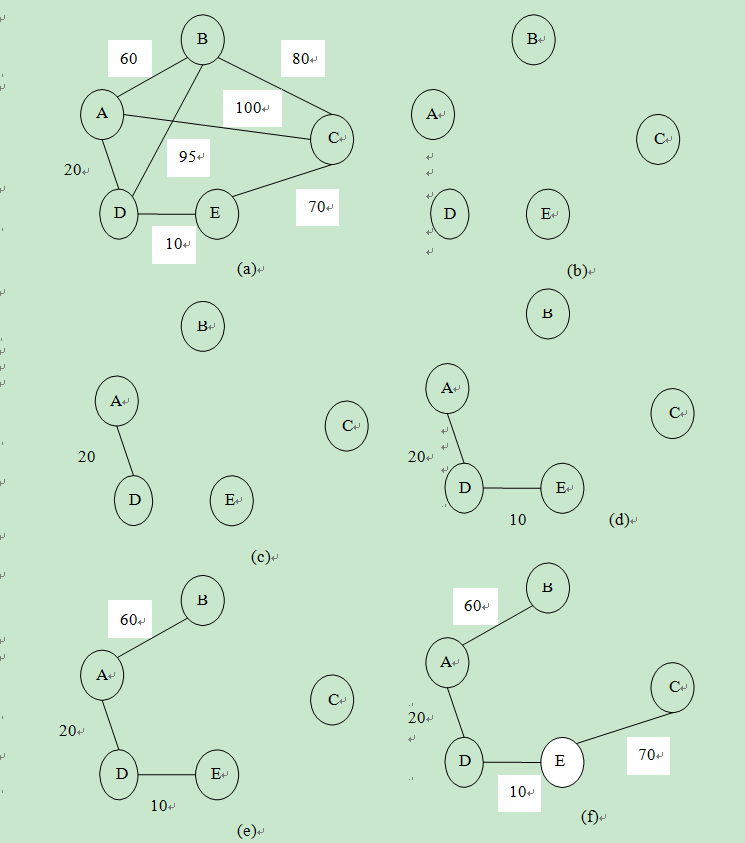
克鲁斯卡尔(Kruskal)算法:对一个有 n 个顶点的无向连通网,将图中的 边按权值大小依次选取,若选取的边使生成树不形成回路,则把它加入到树中; 若形成回路,则将它舍弃。如此进行下去,直到树中包含有 n-1 条边为止。
最短路径:狄克斯特拉(Dikastra)算法:设置 两个顶点的集合 S 和 T,集合 S 中存放已找到最短路径的顶点,集合 T 中存放当 前还未找到最短路径的顶点。初始状态时,集合 S 中只包含源点,设为 v0,然 后从集合 T 中选择到源点 v0 路径长度最短的顶点 u 加入到集合 S 中,集合 S 中 每加入一个新的顶点 u 都要修改源点 v0 到集合 T 中剩余顶点的当前最短路径长 度值,集合 T 中各顶点的新的最短路径长度值为原来的当前最短路径长度值与 从源点过顶点 u 到达该顶点的新的最短路径长度中的较小者。此过程不断重复, 直到集合 T 中的顶点全部加到集合 S 中为止。