再学斐波那契数列

        递归算法在实际应用中司空见惯，斐波那契数列是具体体现之一，递归算法是基本技能，今天是周六，再动一下大脑~

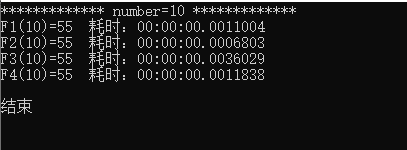
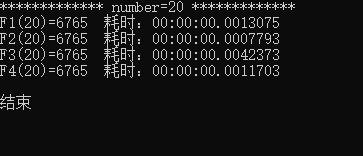
     F1：迭代法，F2：直接法，F3矩阵法，F4：通项公式

using System;
using System.Diagnostics;


namespace Fibonacci
{
    class Program
    {
        static void Main(string[] args)
        {
            ulong result;

            int number = 10;
            Console.WriteLine("************* number={0} *************", number);

            Stopwatch watch1 = new Stopwatch();
            watch1.Start();
            result = F1(number);
            watch1.Stop();
            Console.WriteLine("F1({0})=" + result + "  耗时：" + watch1.Elapsed, number);

            Stopwatch watch2 = new Stopwatch();
            watch2.Start();
            result = F2(number);
            watch2.Stop();
            Console.WriteLine("F2({0})=" + result + "  耗时：" + watch2.Elapsed, number);

            Stopwatch watch3 = new Stopwatch();
            watch3.Start();
            result = F3(number);
            watch3.Stop();
            Console.WriteLine("F3({0})=" + result + "  耗时：" + watch3.Elapsed, number);

            Stopwatch watch4 = new Stopwatch();
            watch4.Start();
            double result4 = F4(number);
            watch4.Stop();
            Console.WriteLine("F4({0})=" + result4 + "  耗时：" + watch4.Elapsed, number);

            Console.WriteLine();

            Console.WriteLine("结束");
            Console.ReadKey();
        }

        /// <summary>
        /// 迭代法
        /// </summary>
        /// <param name="number"></param>
        /// <returns></returns>
        private static ulong F1(int number)
        {
            if (number == 1 || number == 2)
            {
                return 1;
            }
            else
            {
                return F1(number - 1) + F1(number - 2);
            }
            
        }

        /// <summary>
        /// 直接法
        /// </summary>
        /// <param name="number"></param>
        /// <returns></returns>
        private static ulong F2(int number)
        {
            ulong a = 1, b = 1;
            if (number == 1 || number == 2)
            {
                return 1;
            }
            else
            {
                for (int i = 3; i <= number; i++)
                {
                    ulong c = a + b;
                    b = a;
                    a = c;
                }
                return a;
            }
        }

        /// <summary>
        /// 矩阵法
        /// </summary>
        /// <param name="n"></param>
        /// <returns></returns>
        static ulong F3(int n)
        {
            ulong[,] a = new ulong[2, 2] { { 1, 1 }, { 1, 0 } };
            ulong[,] b = MatirxPower(a, n);
            return b[1, 0];
        }

        #region F3
        static ulong[,] MatirxPower(ulong[,] a, int n)
        {
            if (n == 1) { return a; }
            else if (n == 2) { return MatirxMultiplication(a, a); }
            else if (n % 2 == 0)
            {
                ulong[,] temp = MatirxPower(a, n / 2);
                return MatirxMultiplication(temp, temp);
            }
            else
            {
                ulong[,] temp = MatirxPower(a, n / 2);
                return MatirxMultiplication(MatirxMultiplication(temp, temp), a);
            }
        }

        static ulong[,] MatirxMultiplication(ulong[,] a, ulong[,] b)
        {
            ulong[,] c = new ulong[2, 2];
            for (int i = 0; i < 2; i++)
            {
                for (int j = 0; j < 2; j++)
                {
                    for (int k = 0; k < 2; k++)
                    {
                        c[i, j] += a[i, k] * b[k, j];
                    }
                }
            }
            return c;
        }
        #endregion

        /// <summary>
        /// 通项公式法
        /// </summary>
        /// <param name="n"></param>
        /// <returns></returns>
        static double F4(int n)
        {
            double sqrt5 = Math.Sqrt(5);
            return (1/sqrt5*(Math.Pow((1+sqrt5)/2,n)-Math.Pow((1-sqrt5)/2,n)));
        }
    }
}