You are given n rectangles on a plane with coordinates of their bottom left and upper right points. Some (n−1) of the given n
rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.
Find any point with integer coordinates that belongs to at least (n−1)
given rectangles.
Input
The first line contains a single integer n(2≤n≤132674) — the number of given rectangles.
Each the next n lines contains four integers x1, y1, x2 and y2 (−109≤x1<x2≤109, −109≤y1<y2≤109) — the coordinates of
the bottom left and upper right corners of a rectangle.
Output
Print two integers x
and y — the coordinates of any point that belongs to at least (n−1)
given rectangles.
Examples
3
0 0 1 1
1 1 2 2
3 0 4 1
1 1
3
0 0 1 1
0 1 1 2
1 0 2 1
1 1
4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4
1 1
5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2
3 4
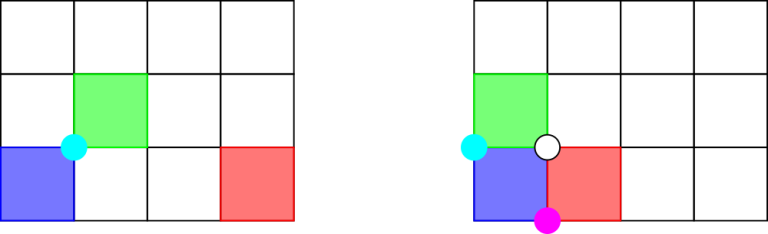
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.
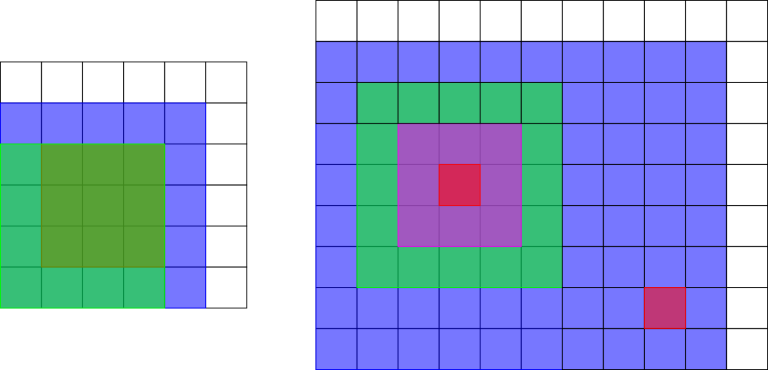
The picture below shows the rectangles in the third and fourth samples.
暴力枚举+线段树优化
只要满足左下角的坐标的最小值大于等于右上角的坐标的最大值一定有公共区间
#include <bits/stdc++.h> using namespace std; #define INF 0x3f3f3f3f int a[150000][4],n; int tree[4][150000<<2]; void build(int l,int r,int root,int dep) { tree[dep][root]=dep>1?INF:-INF; if(l==r){ tree[dep][root]=a[l][dep]; return ; } int mid=l+r>>1; build(l,mid,root<<1,dep); build(mid+1,r,root<<1|1,dep); tree[dep][root]=dep>1?min(tree[dep][root<<1],tree[dep][root<<1|1]):max(tree[dep][root<<1],tree[dep][root<<1|1]); } int query(int l,int r,int root,int L,int R,int dep) { if(L>R) return dep>1?INF:-INF; if(L<=l && R>=r){ return tree[dep][root]; } int ans=dep>1?INF:-INF,mid=l+r>>1; if(L<=mid) ans=dep>1?min(ans,query(l,mid,root<<1,L,R,dep)):max(ans,query(l,mid,root<<1,L,R,dep)); if(R>mid) ans=dep>1?min(ans,query(mid+1,r,root<<1|1,L,R,dep)):max(ans,query(mid+1,r,root<<1|1,L,R,dep)); return ans; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++){ for(int j=0;j<4;j++) scanf("%d",&a[i][j]); } for(int i=0;i<4;i++) build(1,n,1,i); for(int i=1;i<=n;i++) { int b[4]; for(int j=0;j<4;j++){ if(j>1) b[j]=min(query(1,n,1,1,i-1,j),query(1,n,1,i+1,n,j)); else b[j]=max(query(1,n,1,1,i-1,j),query(1,n,1,i+1,n,j)); } if(b[0]<=b[2] && b[1]<=b[3]) return printf("%d %d ",b[0],b[1]),0; } return 0; }