直观理解神经网络最后一层全连接+Softmax

博客：blog.shinelee.me | 博客园 | CSDN

目录

• 写在前面
• 全连接层与Softmax回顾
• 加权角度
• 模板匹配
• 几何角度
• Softmax的作用
• 总结
• 参考

写在前面

这篇文章将从3个角度：加权、模版匹配与几何来理解最后一层全连接+Softmax。掌握了这3种视角，可以更好地理解深度学习中的正则项、参数可视化以及一些损失函数背后的设计思想。

全连接层与Softmax回顾

深度神经网络的最后一层往往是全连接层+Softmax（分类网络），如下图所示，图片来自StackExchange。

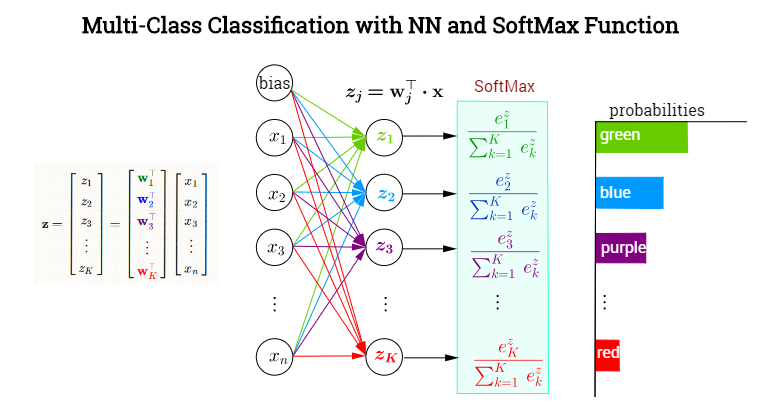
先看一下计算方式：全连接层将权重矩阵与输入向量相乘再加上偏置，将(n)个((-infty, +infty))的实数映射为(K)个((-infty, +infty))的实数（分数）；Softmax将(K)个((-infty, +infty))的实数映射为(K)个((0, 1))的实数（概率），同时保证它们之和为1。具体如下：

[hat{mathrm{y}} = softmax(mathrm{z}) = softmax(mathrm{W}^{T} mathrm{x} + mathrm{b}) ]

其中，(mathrm{x}) 为全连接层的输入，(W_{n imes K}) 为权重，(mathrm{b})为偏置项，(hat{mathrm{y}})为Softmax输出的概率，Softmax的计算方式如下：

[softmax(z_j) = frac{e^{z_j}}{sum_K e^{z_j}} ]

若拆成每个类别的概率如下：

[hat{y_j} = softmax(z_j) = softmax(mathrm{w}_{j} cdot mathrm{x} + b_j) ]

其中，(mathrm{w}_{j})为图中全连接层同一颜色权重组成的向量。

该如何理解？

下面提供3个理解角度：加权角度、模版匹配角度与几何角度

加权角度

加权角度可能是最直接的理解角度。

通常将网络最后一个全连接层的输入，即上面的(mathrm{x})，视为网络从输入数据提取到的特征。

[z_j = mathrm{w}_{j} cdot mathrm{x} + b_j = w_{j1} x_1 + w_{j2} x_2 + dots + w_{jn} x_n + b_j ]

将(mathrm{w}_{j})视为第(j)类下特征的权重，即每维特征的重要程度、对最终分数的影响程度，通过对特征加权求和得到每个类别的分数，再经过Softmax映射为概率。

模板匹配

也可以将(mathrm{w}_{j})视为第(j)类的特征模板，特征与每个类别的模板进行模版匹配，得到与每个类别的相似程度，然后通过Softmax将相似程度映射为概率。如下图所示，图片素材来自CS231n。

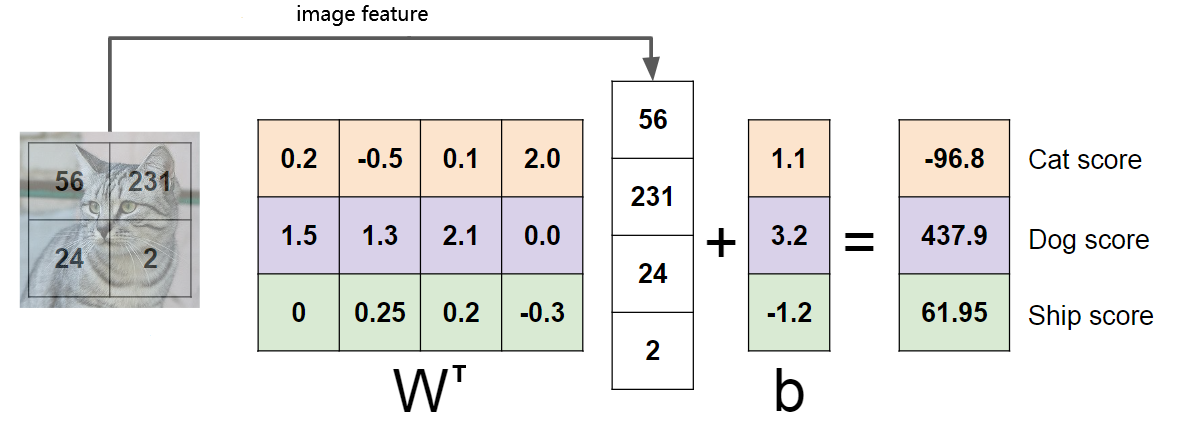
如果是只有一个全连接层的神经网络（相当于线性分类器），将每个类别的模板可以直接可视化如下，图片素材来自CS231n。

如果是多层神经网络，最后一个全连接层的模板是特征空间的模板，可视化需要映射回输入空间。

几何角度

仍将全连接层的输入(mathrm{x})视为网络从输入数据提取到的特征，一个特征对应多维空间中的一个点。

如果是二分类问题，使用线性分类器(hat{y} = mathrm{w} cdot mathrm{x} + b)，若(hat{y}>0)即位于超平面的上方，则为正类，(hat{y}<0)则为负类。

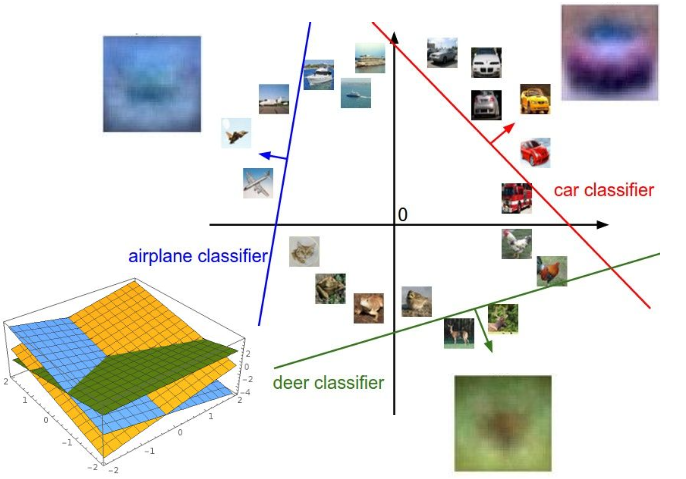
多分类怎么办？为每个类别设置一个超平面，通过多个超平面对特征空间进行划分，一个区域对应一个类别。(mathrm{w}_{j})为每个超平面的法向量，指向正值的方向，超平面上分数为0，如果求特征与每个超平面间的距离（带正负）为

[d_j = frac{mathrm{w}_{j} cdot mathrm{x} + b_j}{||mathrm{w}_{j}||} ]

而分数(z_j = ||mathrm{w}_{j}|| d_j)，再进一步通过Softmax映射为概率。

如下图所示：

Softmax的作用

相比((-infty, +infty))范围内的分数，概率天然具有更好的可解释性，让后续取阈值等操作顺理成章。

经过全连接层，我们获得了(K)个类别((-infty, +infty))范围内的分数(z_j)，为了得到属于每个类别的概率，先通过(e^{z_j})将分数映射到((0, +infty))，然后再归一化到((0 ,1))，这便是Softmax的思想：

[hat{y_j} = softmax(z_j) = frac{e^{z_j}}{sum_K e^{z_j}} ]

总结

本文介绍了3种角度来更直观地理解全连接层+Softmax，

• 加权角度，将权重视为每维特征的重要程度，可以帮助理解L1、L2等正则项
• 模板匹配角度，可以帮助理解参数的可视化
• 几何角度，将特征视为多维空间中的点，可以帮助理解一些损失函数背后的设计思想（希望不同类的点具有何种性质）

视角不同，看到的画面就不同，就会萌生不同的idea。有些时候，换换视角问题就迎刃而解了。

以上。

参考

• CS231n: Convolutional Neural Networks for Visual Recognition