前言:这里将主要介绍的是直接插入排序和改进后的插入排序也称为希尔排序
直接插入排序 (时间复杂度为O(N^2))
介绍:
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
方式一步骤:
1.从第一个元素开始,该元素可以认为已经被排序
2.取出下一个元素,在已经排序的元素序列中从后向前扫描
3.如果该元素(已排序)大于新元素,将该元素移到下一位置
4.重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
5.将新元素插入到该位置中
6.重复步骤2
只有文字的描述还是略显的不太清晰,老规矩看图:
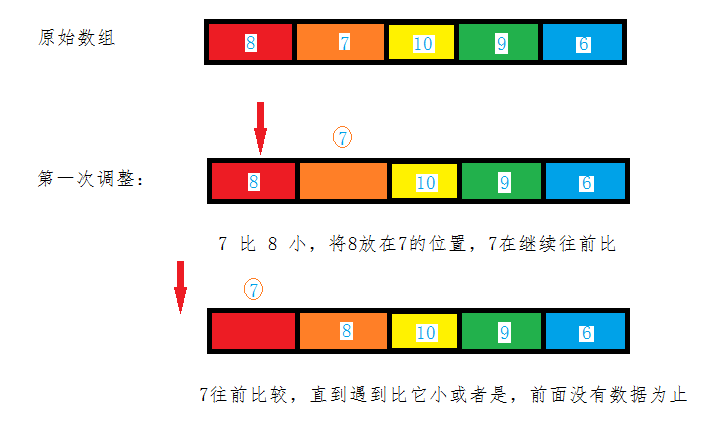
实现的源代码如下:
void InsertSort(T1 * arr, size_t size) //传入的参数是数组的首地址,数组的大小 { assert(arr); for (int i = 1; i < size; ++i) { int end = i - 1; T1 tmp = arr[i]; while (end >= 0 && arr[end] > tmp) //end >= 0 确保的是上图中的红色箭头一直指向数组的有效地址,arr[end] > tmp 代表箭头指向的数大于圆圈中的数 { arr[end + 1] = arr[end]; --end; } arr[end + 1] = tmp; } }
方式二:(是在方式一的基础上进行了一些优化)
思想是这样子滴:
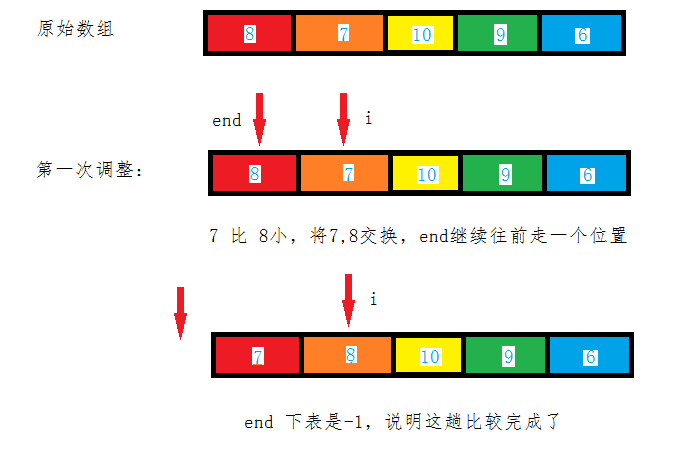
源代码如下:
void _Insert(int* arr, int size) { assert(arr); for (int i = 1; i < size; ++i) { for (int end = i - 1; end >= 0; --end) { if (arr[end] > arr[end + 1]) //如果说,发现后面的比前面的小说明需要进行交换了 swap(arr[end], arr[end + 1]); else break; //否则说明 i之前的序列已经是有序的了 } } }
希尔排序:(时间复杂度为 O(N^1.3))
介绍:希尔排序的实质就是分组插入排序,该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
基本思想:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
如图:
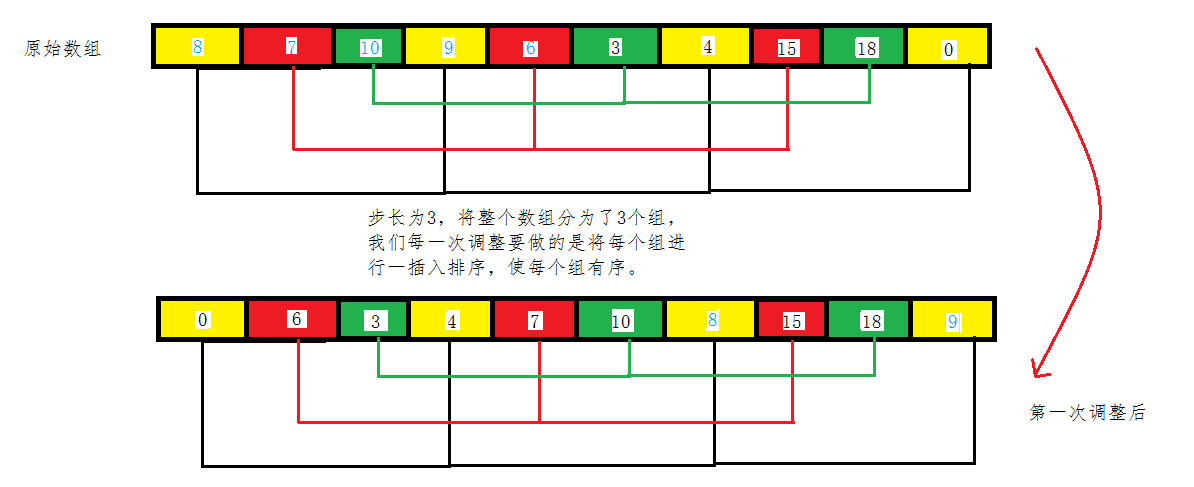
源代码:
void _ShellSort(int * arr, int size) { assert(arr); int gap = size; while (gap > 1) { gap = gap / 3 + 1; //(调整步长)库中的步长是这样计算滴,当步长为 1 时其实就是一个直接插入排序 for (int i = gap; i < size; ++i) { int end = i - gap; int tmp = arr[i]; while (end >= 0 && arr[end] > tmp) { arr[end + gap] = arr[end]; end -= gap; } arr[end + gap] = tmp; } } }
//与直接插入排序类似,改进后的希尔排序也可以这样写:
void _ShellSort(int * arr, int size) { assert(arr); int gap = size; while (gap > 1) { gap = gap / 3 + 1; for (int i = gap; i < size; ++i) { for (int end = i - gap; end >= 0; end -= gap) { if (arr[end] > arr[end + gap]) //如果不满足升序,则交换两个数 { swap(arr[end], arr[end + gap]); } else //否则就认为,i 所在组,在i之前的所有元素都已经是升序了 { break; } } } } }
现在呢,插入排序写的差不多的,你如果还有什么更好的想法、意见或者建议的,欢迎参与评论,跪求赐教~~