一 、支持向量机(SVM)
1.1 符号定义
标签 y 不再取 0 或 1,而是: y∈{-1, 1}
定义函数:
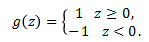
向量,没有第 0 个维度,b 为截距,预测函数定义为:

1.2 函数间隔与几何间隔
1.2.1 函数间隔
样本个体:

全体:

1.2.2 几何间隔
样本个体:

全体:
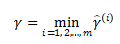
1.2.3 关系
函数间隔与几何间隔都是对预测置信度的度量,这个间隔越大,说明预测样本离着分界线越远,我们预测的结果也就更加可靠。

1.3 优化目标
假设样本是线性可分的,优化目标为
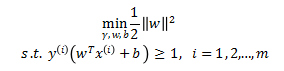
1.4 广义拉格朗日乘数法
带约束的优化为:
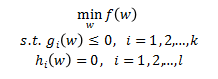
转化为:
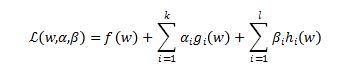
【原始问题】:
记量 为:
为: 
原始问题为:
【对偶问题】:
记量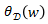 为:
为: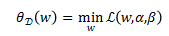
对偶问题为: 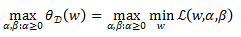
对于原始问题和对偶问题,以下关系恒成立:
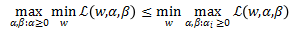
KKT条件:

当KKT条件满足时,对偶问题和原始问题有着相同的解。
1.5 最优间隔分类器
SVM的拉格朗日乘数法:
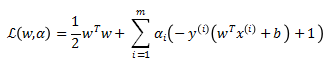
原始问题:
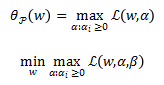
对偶问题:

根据KKT条件:
对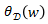 关于
关于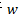 求梯度,令之为0,可得:
求梯度,令之为0,可得:
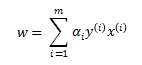
对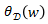 关于 b 求导,令之为0,可得:
关于 b 求导,令之为0,可得:
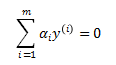
带回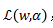 ,得:
,得:

因此SVM的对偶问题为:

将对偶解 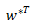 带入原始问题,对所有的
带入原始问题,对所有的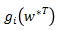 不等于 0 对应的系数
不等于 0 对应的系数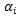 求导,令其等于0,得:
求导,令其等于0,得:

因为 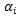 不为的项
不为的项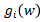 为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于
为0,即该点为支持向量。理想情况分割线两侧各有一个最近的点,且我们也仅在两侧各取一个点。因此,对于 的,两侧同时乘 -1,累加两个式子得:
的,两侧同时乘 -1,累加两个式子得:
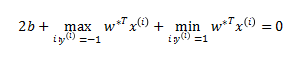
即:

上述算法称为最优间隔分类器。
1.6 SVM核
将 中的内积
中的内积 替换为
替换为 ,称
,称 为核。核 K 的合法取法有很多,如:
为核。核 K 的合法取法有很多,如:
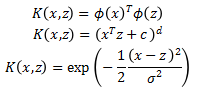
不同的核将 x 和 z 映射到了不同的空间之中,一组低维的向量投射至高维通常更容易划分。
1.7  正则化与软间隔
正则化与软间隔
对于一些线性不可分的情况,或者为了抵制噪音的影响,使用 软边距进行处理。为每组数据加入一个允许误差
软边距进行处理。为每组数据加入一个允许误差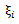 ,同时在优化目标中加入惩罚项
,同时在优化目标中加入惩罚项 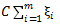 。SVM的原始优化问题变为:
。SVM的原始优化问题变为:
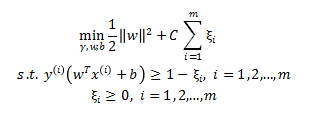
拉格朗日乘数法写作:
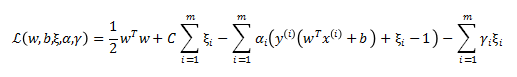
根据KKT条件,
令 ,得:
,得: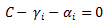
令 ,得:
,得:
令 ,得:
,得:
同样求对偶问题得到:

根据KKT条件, 取值的关系如下:
取值的关系如下:
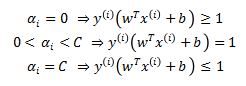
注意,b 不再是原始SVM的取值。
【Reference】
1. 支持向量机通俗导论(理解SVM的三层境界) 【这篇写的非常好】