我们能得到一个函数f在区间[a,b]上某些点的值或者这些点上的高阶导数
我们就能通过插值法去得到一个函数g,g与f是非常相近的
一般来说g分为三类,一类是n次多项式 an*xn + an-1*xn-1 + .......+a0,一类是三角多项式,最后一类是分段n次多项式
多项式插值
这个可以说是最简单的插值了
对于an*xn + an-1*xn-1 + .......+a0,我们有n+1个未知数,我只需要知道n+1个点的函数值就可以解出这n+1个未知数
将解出的值带入即可
优点:简单粗暴
缺点:要解n+1个方程,时间复杂度较高,n不好确定,若n过大,容易过拟合,若n过小,容易欠拟合
拉格朗日插值
先说一阶多项式
我们有两点式
f(x) = yk*(xk+1 - x) / (xk-xk+1) + yk+1*(x-xk) / (xk+1 - xk)
此两点式可以看做∂ * yk + (1-∂) * yk+1
那么自然的在x=xk的时候 ∂=0 在x=xk+1的时候∂=1
这里的∂其实是与x相关的一阶多项式
再说二阶多项式
对于一个二次函数,我们有三个点(xk-1,yk-1) ,(xk,yk) ,(xk+1,yk+1)
我们有lk-1,lk,lk+1
f(x) = lk-1*yk-1 + lk*yk + lk+1*yk+1
其中l是与x相关的二次多项式
我们可以把l当作基函数
这样的话就有
x = xk-1 时lk-1 = 1, lk=0, lk+1 = 0
x = xk时 lk-1 = 0, lk=1, lk+1 = 0
x = xk+1时lk-1 = 0, lk=0, lk+1 = 1
那么这个插值基函数是很好求的
因为每个插值函数都有两个零点
对于lk-1来说有零点xk,xk+1
那么lk-1就可以表示为lk-1 = A*(x-xk)*(x-xk+1)
因为x=xk-1时lk-1 = 1
所以A = 1 / ((xk-1 - xk)* (xk-1 - xk+1) )
那么同理lk和lk+1也能求出来了
那我们得到二阶的拉格朗日插值多项式
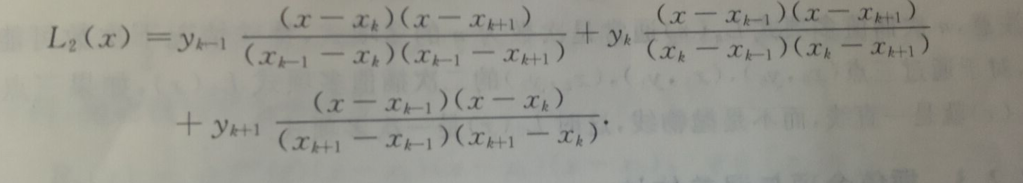
现在将二阶推广到n阶
得到n接的拉格朗日插值多项式
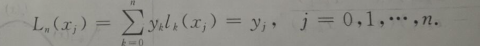

余项:
Rn(x) = f(x) - Ln(x) Rn(x)表示n次拉格朗日多项式的插值余项
Rn(x) = fn+1(e)/(n+1)! * wn+1(x) e属于[a,b]且依赖与x wn+1(x) = (x-x0)(x-x1).......(x-xn)
优点:算法较为简单
缺点:无法处理动态增加节点的情况
牛顿插值
还是先从一阶到二阶进行说明
我先得到了一阶差值多项式P1(x),P1(x) 满足过点(x1, f(x1)), (x2,f(x2))
假设现在有第三个点(x3,f(x3))我们要通过这个点去得到二阶差值多项式P2(x) 使得P2(x)过这三个点
可以设P2(x) = P1(x) + a2*(x-x0)*(x-x1)
通过第三个点解出a2就行了
推广到多阶
那么可以得到Pn(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + a3(x-x0)(x-x1)(x-x2) + ......
求这个插值多项式的值可以通过递推一步一步的求
这样就实现了动态增删
可以看到计算ak需要计算(k-1)2次,那么牛顿插值法就是一个快速的计算方法
均差
一阶均差 f[x0, xk] = ( f(xk) - f(x0) ) / (xk - x0)
二阶均差 f[x0, x1, x2] = (f[x0, x2] -f[x0, x1] ) / (x2 - x1)
可以看到一阶均差就是简单的求斜率
二阶均差就是对一阶均差求斜率
那么k阶均差就是
f[x0, x1,,,,,,xk] = (f[x0,,,,,xk-2, xk] -f[x0, ,,,,,,,xk-2,xk-1] ) / (xk - xk-1)
f[x0, x1,,,,,,xk] = fn(ε) / n!
均差的性质
k阶均差可表示为f(x0),f(x1), f(x2),,,,,,,,, f(xk)的线性组合
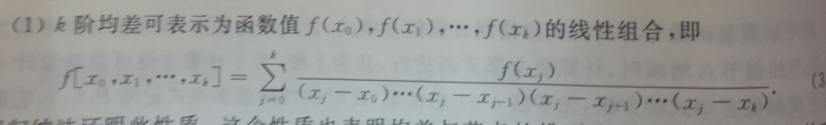
牛顿插值中的a就是均差,可以从一阶开始推,然后使用数学归纳法证明
那么牛顿插值多项式就是:
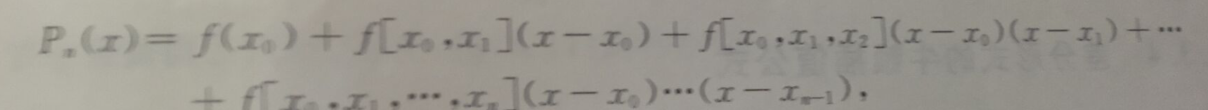
在计算f[x0,x1,,,,,,,,,,xn]时,一般使用均差表
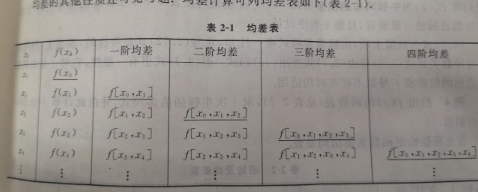
均差表的计算方式为
a[i,j] = ( a[i-1][j] - a[i-1][j-1] ) / (末尾的x - 最开始的x)
误差:
误差为最后一阶的均差 * w(x)
优点:可动态增删节点
缺点:无法处理要求导数相同的情况
埃尔米特插值法实验报告
一个点,多个导数:
牛顿插值中的均差在xi->x0时其实分别是i阶导数,这样就是我们熟悉的泰勒多项式
此时的插值函数就是泰勒多项式
![]()
两个点,一个导数
我们有三个条件,也就是说我们能求出三次插值多项式
这时我们先写出过这两个点的牛顿插值多项式
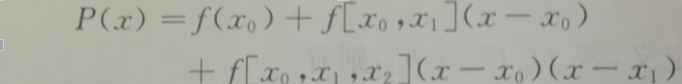
在这个多项式的基础上我们再加上一个三次项
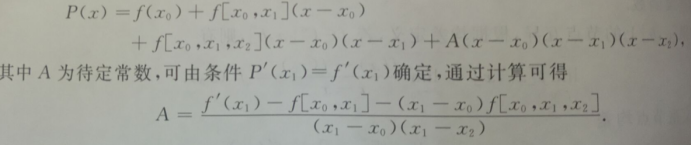
搞定,可以观察到,这三个项数其实可以算是正交的,因为当x=x1或者x=x2时最后一项是0满足条件的
两个点,两个导数
这也是题目所要求的情况
因为有两个导数,所以牛顿插值法无法解决,这里只能使用基函数方法
设插值函数为H(x), 点与导数分别为(x1,y1,m1),(x2,y2,m2)
H(x)满足:H(x1) =y1, H(x2) = y2, H(x1)’ = m1,H(x2)=m2
H(x) = a1*x1 + a2*x2 + b1*m1 + b2*m2
其中 a1, a2, b1, b2均为三层插值多项式
X=x1时 a1(x1) = 1,a2(x1) = 0, b1(x1) = 0,b2(x1) = 0,a1’(x1) = 1,a2’(x1) = 0
X=x2时 a1(x2) = 0,a2(x2) = 1, b1(x2) = 0,b2(x2) = 0,a1’(x2) = 1,a2’(x2) = 0
X=x1时 b1’(x1) = 1,b2’(x1) = 0
X=x2时b1’(x1) = 0,b2’(x1) = 1
然后用了一个很巧妙的方法设基函数,解出来值和就是这样子的
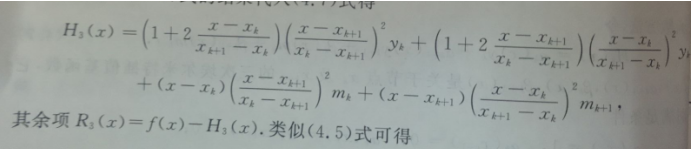
R3(x) = 1/4! * (x-xk)2(x-xk+1)2*f4(ε)
两个点,两个导数2
直接使用泰勒多项式,并把将余项改为未知数,使用多余的一个条件去求余项的值
例如:
求次数小于等于3的多项式P(x),使满足条件
P(x0)=f(x0),P'(x0)=f'(x0),P"(x0)=f"(x0),P(x1)=f(x1)。

多个点,多个一阶导数,三次
两个点作为一个区间每个区间分别求就好啦
这样子还保证了导数的连续性
优点:可保证一阶导数连续
三次样条插值
三次样条插值就是使用 ax3+bx2+cx + d = 0去做拟合
一共有4个未知数,也就是说 对于每个小区间,我需要至少4个方程
假设我有n个点, 那么就一共有n-1个小区间,一共就是4n - 4个方程
因为n个点中,我们有n个点的函数值 n个方程
每个区间相邻点函数值相等 n-2个方程
每个区间相邻点一阶导相等 n-2个方程
每个区间相邻点二阶导相等 n-2个方程
还差两个条件
剩下的两个条件一般为
区间两端点的一阶导已知
区间两端点的二阶导为0
那么一共是4n - 2个方程,搞定
具体解法:
这里放一个例题


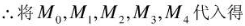

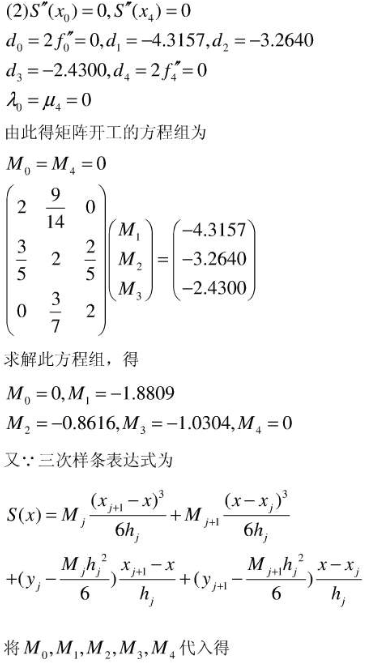

优点:三次样条插值得到的插值函数二阶导,一阶导均连续,此为三次样条插值的