二分类,我们之前使用的激活函数是sigmoid
对于支持向量机来说我们使用的损失函数不同

最后那个1/2 theta^2是正则化项而已
那么为什么这个激活函数能做到大间距分类器呢
当我们训练到一定程度的时候,由于我们cost function 的特性
 可以等于0
可以等于0
那么也就是说只剩下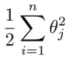
也就是说在训练的后期(分类已经出来了的情况下),我们通过减少最后那一项来得到大间距分类器
为什么减少最后那一项就可以呢
由于常数不重要
我们可以把优化最后一项看做优化theta的范数
分界线其实是与向量(theta1, theta2 ,,,,,thetan)是正交的(这个你简单的画个图就知道了)
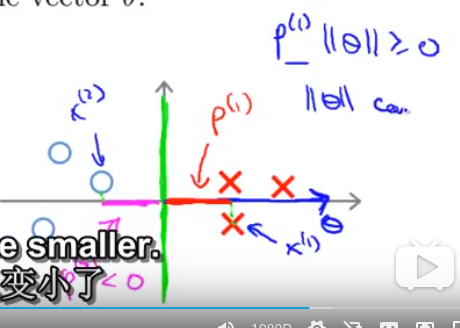
对于小间距分类器来说,我们的样本点向量 与tehta的内积会比较小
对于正向量来说在训练了一段时间之后
xi 与theta 的内积必须大于1
其实也就是xi与theta 的单位方向向量向乘 × theta 的范数
在这种情况下,pi会很小,相对应的来说theta的范数就会很大
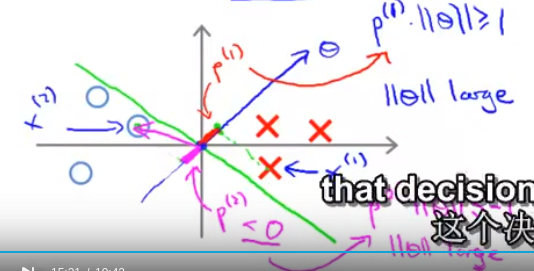
那么对于一个好的分类器
我们要求pi很大,也就是说thetai较小
那么我们在拟合的很好的情况下去min theta的范数就能达到获得大间距分类器的效果