传送门:线段树的区间修改
线段树真是个好东西,查询、更新的时间复杂度均为O(lgN),可以说十分平衡了。
线段树考点还挺多的,区间合并,扫描线也都是线段树的引用,还是需要好好看看的。
因为时间原因,也来不及仔细研究,只能够囫囵吞枣了。
题意:
线段树--区间替换区间求和 教程
思路:
区间替换引入了 懒惰标记这一概念,使得不需要更新所有的点,为暂时不需要更新的点打上标记即可。
等下次需要更新的时候,再将懒惰标记下放。
若无懒惰标记,修改区间[3,9]的话,所有绿色的点都应当更新
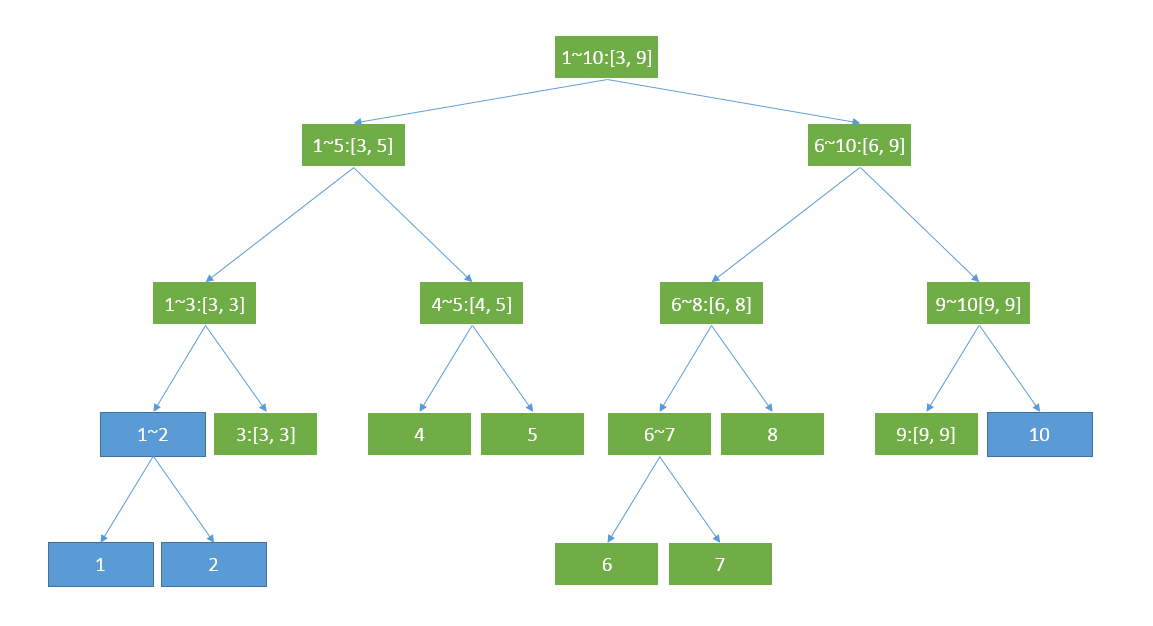
有懒惰标记的话,修改区间[3,9],只需更新黄色结点,并为其标上相应地tag
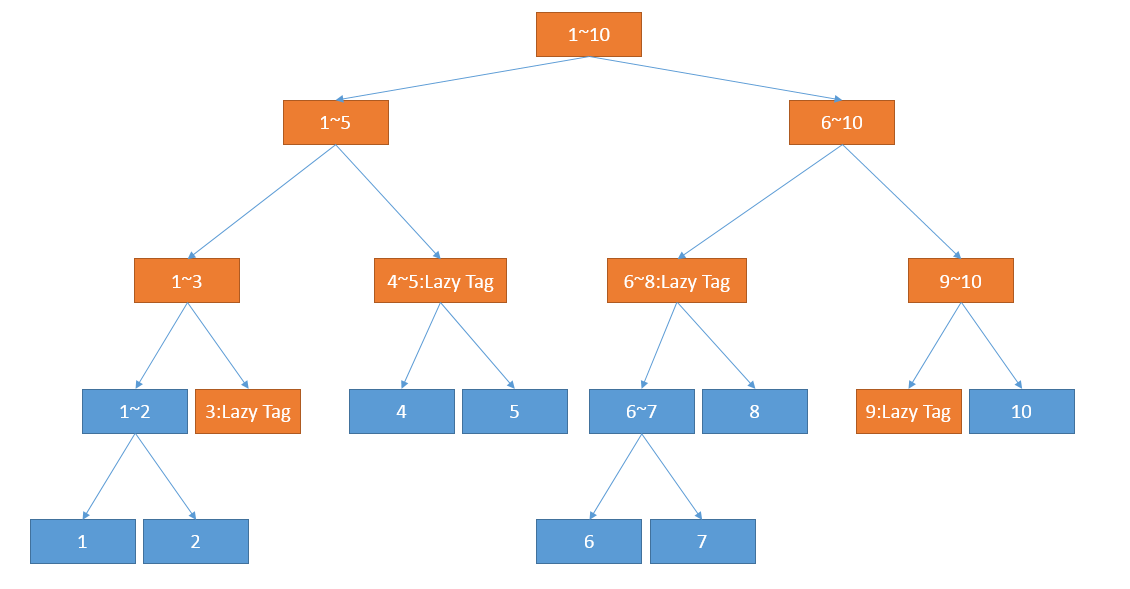
Online AC Code
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAX=1008600;
int sum[MAX<<2],flag[MAX<<2];
inline void PushUp(int idx)
{
sum[idx]=sum[idx<<1]+sum[idx<<1|1];
}
void Build(int idx,int left,int right)
{
// flag : -1表示没有懒惰标记
flag[idx]=-1;
if(left==right)
{
scanf("%d",sum+idx);
return ;
}
int mid=(left+right)>>1;
Build(idx<<1,left,mid);
Build(idx<<1|1,mid+1,right);
PushUp(idx);
}
// 懒惰标记的‘下放操作’
inline void PushDown(int idx,int left,int mid)
{
int L=idx<<1,R=L+1;
sum[L]=(mid-left+1)*flag[idx];
sum[R]=sum[idx]-sum[L];
flag[L]=flag[R]=flag[idx];
flag[idx]=-1;
}
int L,R,val;
void Update(int idx,int left,int right)
{
if(L<=left && right<=R)
{
sum[idx]=(right-left+1)*val;
// 放置懒惰标记
flag[idx]=val;
return;
}
int mid=(left+right)>>1;
if(flag[idx]!=-1) PushDown(idx,left,mid);
if(L<=mid) Update(idx<<1,left,mid);
if(mid<R) Update(idx<<1|1,mid+1,right);
PushUp(idx);
}
int Query(int idx,int left,int right)
{
if(L<=left && right<=R)
return sum[idx];
int mid=(left+right)>>1,ans=0;
if(flag[idx]!=-1) PushDown(idx,left,mid);
if(L<=mid) ans+=Query(idx<<1,left,mid);
if(mid<R) ans+=Query(idx<<1|1,mid+1,right);
return ans;
}
int main()
{
//freopen("test.txt","r",stdin);
int N,i,M;
scanf("%d",&N);
Build(1,1,N);
scanf("%d",&M);
while(M--)
{
scanf("%d%d%d",&i,&L,&R);
if(i)
{
scanf("%d",&val);
Update(1,1,N);
}
else printf("%d
",Query(1,1,N));
}
return 0;
}