[NOI2013]矩阵游戏

　

对于不会矩阵乘法的孩子，你们有救啦。（矩阵乘法版直接拉到下面）

【分析】

我们先从简单的来推。考虑第一行。

我们可以根据等比数列推出通项式（纸上划划就行了）

然而这只是第一步。

上述公式其实是建立在f[i][x]上的。

根据f[i][m]和f[i+1][1]的公式，我们可以推出f[i+1][1]和f[i][1]的关系。（其实只要再乘上c，加上d即可）

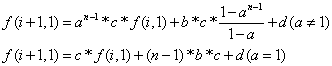(这里的n其实是m（打错了）)

然后是不是有发现了一个规律？把和a，b，c，d有关的全部当成常数，这个公式可以变成最上面的那个公式！这样，我们可以轻松的求出f[x][1]的值。

之后有两个方法：

求出f[n][1]并递推至f[n][m];

求出f[n+1][1]后，减去d除以c。

我选了第二种。虽然快了一点，但是还要求逆元。（都做到这种份上了，逆元也不过如此了）

到此为止，就求完了。

【注意】

①因为n和m的范围很大，我们要用到费马小定理。

　　

　　x^a=x^(a%phi(p)+phi(p)) (mod p)

ps:n,m在指数中出现时才可用费马小定理，系数中出现不能用！！！

这样，我们可以把n先对（p-1）取模，再计算。（因为除掉的那些乘积是1）

②对于a=1的情况要特判。

 

#include<cstdio>
#include<cstring>
 
using namespace std;
typedef long long ll;
 
#define setfire(name) freopen(#name".in","r",stdin);freopen(#name".out","w",stdout);
#define fre(name) freopen(#name".txt","r",stdin);
#ifdef WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
 
const int N=1e6+5;
const ll mod=1e9+7;
char s1[N],s2[N];
struct data{ll uni,ord;}n,m;
ll a,b,c,d,e,f,g;
 
void get_num(char *s,data &a){
    int p=strlen(s);ll x=0;
    for(int i=0;i<p;i++){
        a.uni=(a.uni*10+s[i]-'0')%mod;
        a.ord=(a.ord*10+s[i]-'0')%(mod-1);
    }
}
ll fpow(ll a,ll p){
    ll res=1;
    for(;p;p>>=1,a=a*a%mod) if(p&1) res=res*a%mod;
    return res;
}
ll inv(ll x){
    return fpow(x,mod-2);
}
int main(){
    setfire(matrixb);
    scanf("%s%s",s1,s2);
    get_num(s1,n);get_num(s2,m);
    scanf(LL LL LL LL,&a,&b,&c,&d);
    if(a==1){
        a=c;
        b=((m.uni-1)*b%mod*c+d)%mod;
    }
    else{
        g=b*inv(a-1)%mod;
        e=fpow(a,m.ord-1);
        a=e*c%mod;
        b=((e-1)*g%mod*c%mod+d)%mod;
    }
    if(a==1){
        f=(1+n.uni*b)%mod;
    }
    else{
        g=b*inv(a-1)%mod;
        e=fpow(a,n.ord);
        f=(e+(e-1)*g)%mod;
    }
    printf(LL,((f-d)*inv(c)%mod+mod)%mod);
    return 0;
}

 

矩阵乘法版

【分析】

很容易推出，A{a,b}    B{c,d}

{0,1}       {0,1}

A^(m-1)

B=B*A

B=B^(n-1)

A=A*B

 

Ans=A[0][0]+A[0][1]

Ps:考虑到A,B的第二行不会对答案造成贡献，直接删去，优化矩阵乘法的常数。

{c,d}*{a,b}={a*c,b*c+d}

 

#include<cstdio>
using namespace std;
typedef long long ll;
 
#define setfire(name) freopen(#name".in","r",stdin);freopen(#name".out","w",stdout);
#define fre(name) freopen(#name".txt","r",stdin);
#ifdef WIN32
#define LL "%I64d"
#else
#define LL "%lld"
#endif
 
const int N=1e6+5;
const ll mod=1e9+7;
struct M{ll x,y;}A,B,C;
char s1[N],s2[N];ll n,m,a,b,c,d,phi;
 
M operator *(const M &a,const M &b){
    return (M){a.x*b.x%mod,(a.x*b.y+a.y)%mod};
}
M operator ^(M a,ll p){
    M f=a;
    for(p--;p;p>>=1,a=a*a) if(p&1) f=f*a;
    return f;
}
void get(char *s,ll &num){
    for(int i=0;s[i];i++){
        num=(num*10+s[i]-'0')%phi;
    }
}
int main(){
    setfire(matrixb)
    scanf("%s%s",s1,s2);
    scanf(LL LL LL LL,&a,&b,&c,&d);
    if(a==1&&c==1) phi=mod;else phi=mod-1;
    get(s1,n);get(s2,m);
    A=(M){a,b};B=(M){c,d};
    
    A=A^(m-1);
    B=B*A;
    B=B^(n-1);
    A=A*B;
    
    printf(LL ,(A.x+A.y)%mod);
    return 0;
}