BZOJ 3505

3505: [Cqoi2014]数三角形

Time Limit: 10 Sec  Memory Limit: 128 MB
Submit: 1171  Solved: 703
[Submit][Status][Discuss]

codevs3693 数三角形同题：http://codevs.cn/problem/3693/

Description

给定一个nxm的网格，请计算三点都在格点上的三角形共有多少个。下图为4x4的网格上的一个三角形。

注意三角形的三点不能共线。

Input

输入一行，包含两个空格分隔的正整数m和n。

Output

输出一个正整数，为所求三角形数量。

Sample Input

2 2

Sample Output

76


数据范围
1<=m,n<=1000

HINT

 

Source

题解：

1、先不考虑三角形，从n*m的网格里面任意选取3个点，一共有多少种方案？ C(n*m,3) 现在，这3个点必须要构成三角形，有哪种情况需要去除？ 三点共线的情况。 我们用C(n*m,3)减去三点共线的情况，最后得到的就是答案。

2、一个n*m的网格，有多少种选法，选择3个点是三点共线的？ 这是一个5*7的网格

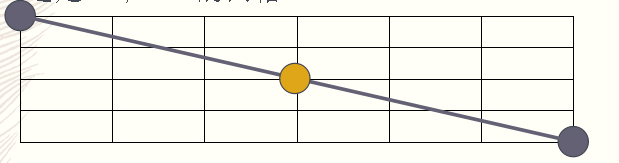
如果固定左上角和右下角这两个点，一共有多少个点和它们共线？

3、

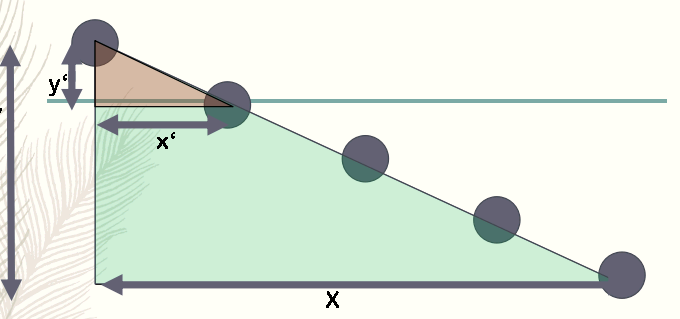
大三角形和小三角形是相似的 小三角形的直角边长x’和y’应该是大三角形的直角边长X和Y的约数 所能放下的点的个数-1是X/x’=Y/y’,这个数也是X的约数，同时也是Y的约数 所以最多能放gcd(X,Y)-1个点。

4、

回到刚才那个问题的话，一个n*m的网格，它的两条边的长度分别是n-1和m-1，所以对角线上最多有gcd(n-1,m-1)-1个点在格线上。 再看这道题本身，我们求有多少种选取三个点的选法，满足三点共线，可以分这两种情况 所在直线水平/竖直 所在直线是斜的

所在直线水平/竖直： n*C(m,3)+m*C(n,3) 所在直线是斜的： 先用一个双重循环，枚举三个点中以两头的两个点为对角线所构成的网格的大小 如果以这两个点为对角线构成了一个n’*m’的网格，则以它们为两头的点，一共有gcd(n’-1,m’-1)-1种选法可以三点共线

5、

AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
#define ll unsigned long long 
ll n,m;
ll gcd(ll a,ll b){
    return !b?a:gcd(b,a%b);
}
ll C(ll x){
    return x*(x-1)/2*(x-2)/3;
}
int main(){
    cin>>n>>m;
    ll ans=C((m+1)*(n+1));
    for(int i=0;i<=n;i++){
        for(int j=0;j<=m;j++){
            if(i||j) ans-=(gcd(i,j)-1)*(n-i+1)*(m-j+1)*(i&&j?2:1);
        }
    }
    cout<<ans<<endl;
    return 0;
}