Codevs 1076 排序
以本题为例,复习各种排序(部分);
题目描述 Description
给出n和n个整数,希望你从小到大给他们排序
第一行一个正整数n
第二行n个用空格隔开的整数
输出仅一行,从小到大输出n个用空格隔开的整数
3
3 1 2
1 2 3
1<=n<=100000
分类标签 Tags 点此展开
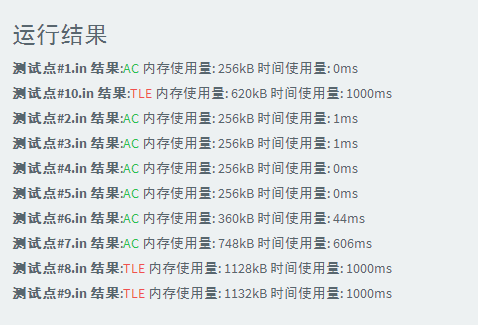
#include<cstdio> using namespace std; #define N 1010000 int a[N],n; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",a+i); } for(int i=2,x;i<=n;i++){ x=a[i];int j=i-1; while(x<a[j]&&j>0){ a[j+1]=a[j]; j--; } a[j+1]=x; } for(int i=1;i<=n;i++){ printf("%d ",a[i]); } return 0; }
2、桶排序
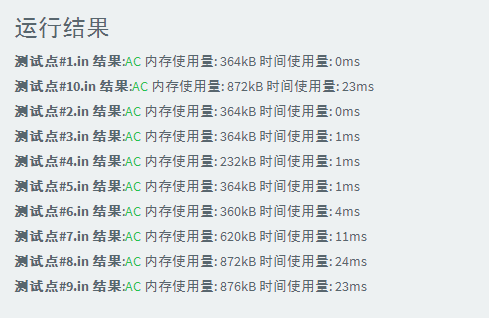
#include<cstdio> #include<iostream> using namespace std; #define N 1010000 int a[N],b,n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&b);a[b]++; } int t=0; for(int i=0;t<n;i++) while(a[i]>0){ printf("%d ",i); a[i]--; t++; } return 0; }
3、快速排序

#include<cstdio> #include<iostream> using namespace std; #define N 1010000 int a[N],n; void quick_sort(int l,int r){ if(l>r) return; int i=l,j=r,mid=a[(l+r)/2];//这里换成mid,下面换成a[mid],就会有错误 while(i<=j){//原因:a[mid]会被更新 while(a[i]<mid) i++; while(a[j]>mid) j--; if(i<=j){ swap(a[i],a[j]); i++;j--; } } if(j>l) quick_sort(l,j); if(i<r) quick_sort(i,r); } int main() { scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",a+i); } quick_sort(1,n); for(int i=1;i<=n;i++){ printf("%d ",a[i]); } return 0; }
stl-sort(c++自带快排)
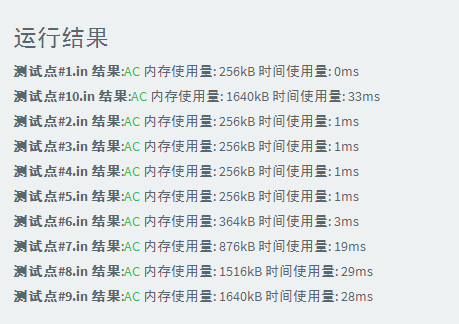
#include<cstdio> #include<algorithm> using namespace std; int a[101000],n; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); sort(a+1,a+n+1); for(int i=1;i<=n;i++) printf("%d ",a[i]); return 0; }
4、归并排序
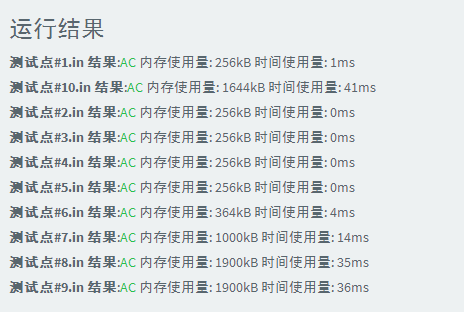
#include<cstdio> #include<iostream> using namespace std; #define N 1001000 int a[N],s[N],n; void merge_sort(int l,int r){ if(l==r) return ; int mid=(l+r>>1); merge_sort(l,mid); merge_sort(mid+1,r); int i=l,j=mid+1,k=l; while(i<=mid&&j<=r){ if(a[i]<=a[j]) s[k++]=a[i++]; else s[k++]=a[j++]; } while(i<=mid) s[k++]=a[i++]; while(j<=r) s[k++]=a[j++]; for(int i=l;i<=r;i++) a[i]=s[i]; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",a+i); merge_sort(1,n); for(int i=1;i<=n;i++) printf("%d ",a[i]); return 0; }
5、堆排序
#include<cstdio> #include<iostream> using namespace std; #define N 1010000 int heap[N],heap_size,n,ans; void put(int x){ int now,next; heap[++heap_size]=x; now=heap_size; while(now>1){ next=now/2; if(heap[next]<=heap[now]) return; swap(heap[next],heap[now]); now=next; } } int get(){ int now,next,res; res=heap[1]; heap[1]=heap[heap_size--]; now=1; while(now*2<=heap_size){ next=now*2; if(next<heap_size&&heap[next+1]<heap[next]) next++; if(heap[now]<=heap[next]) return res; swap(heap[next],heap[now]); now=next; } return res; } int main(){ scanf("%d",&n); for(int i=1,x;i<=n;i++){ scanf("%d",&x); put(x); } for(int i=1,x,y;i<=n;i++){ printf("%d ",get()); } return 0; }
6、缺少:冒泡,拓扑……--其实我的博客有例题,自己搜吧,不在此整理
7、常用排序去重方法
(1)朴素去重
#include<cstdio> #include<algorithm> using namespace std; int a[101],n,f[101]; int main(){ int p,j=1; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&a[i]); sort(a+1,a+n+1); f[j]=a[1]; p=a[1]; for(int i=2;i<=n;i++) if(a[i]!=p) f[++j]=a[i],p=a[i]; printf("%d ",j);//去重后元素个数 for(int i=1;i<=j;i++) printf("%d ",f[i]);//去重后所有元素 return 0; }
(2)STL去重
#include<cstdio> #include<algorithm> using namespace std; #define N 1010 int a[N],n; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",a+i); } sort(a+1,a+n+1); int m=unique(a+1,a+n+1)-(a+1); printf("%d ",m); for(int i=1;i<=m;i++){ printf("%d ",a[i]); } return 0; }
1 快速排序(QuickSort)
快速排序是一个就地排序,分而治之,大规模递归的算法。从本质上来说,它是归并排序的就地版本。快速排序可以由下面四步组成。
(1) 如果不多于1个数据,直接返回。
(2) 一般选择序列最左边的值作为支点数据。
(3) 将序列分成2部分,一部分都大于支点数据,另外一部分都小于支点数据。
(4) 对两边利用递归排序数列。
快速排序比大部分排序算法都要快。尽管我们可以在某些特殊的情况下写出比快速排序快的算法,但是就通常情况而言,没有比它更快的了。快速排序是递归的,对于内存非常有限的机器来说,它不是一个好的选择。
2
归并排序(MergeSort)
归并排序先分解要排序的序列,从1分成2,2分成4,依次分解,当分解到只有1个一组的时候,就可以排序这些分组,然后依次合并回原来的序列中,这样就可以排序所有数据。合并排序比堆排序稍微快一点,但是需要比堆排序多一倍的内存空间,因为它需要一个额外的数组。
3
堆排序(HeapSort)
堆排序适合于数据量非常大的场合(百万数据)。
堆排序不需要大量的递归或者多维的暂存数组。这对于数据量非常巨大的序列是合适的。比如超过数百万条记录,因为快速排序,归并排序都使用递归来设计算法,在数据量非常大的时候,可能会发生堆栈溢出错误。
堆排序会将所有的数据建成一个堆,最大的数据在堆顶,然后将堆顶数据和序列的最后一个数据交换。接下来再次重建堆,交换数据,依次下去,就可以排序所有的数据。
4 Shell排序(ShellSort)
Shell排序通过将数据分成不同的组,先对每一组进行排序,然后再对所有的元素进行一次插入排序,以减少数据交换和移动的次数。平均效率是O(nlogn)。其中分组的合理性会对算法产生重要的影响。现在多用D.E.Knuth的分组方法。
Shell排序比冒泡排序快5倍,比插入排序大致快2倍。Shell排序比起QuickSort,MergeSort,HeapSort慢很多。但是它相对比较简单,它适合于数据量在5000以下并且速度并不是特别重要的场合。它对于数据量较小的数列重复排序是非常好的。
5 插入排序(InsertSort)
插入排序通过把序列中的值插入一个已经排序好的序列中,直到该序列的结束。插入排序是对冒泡排序的改进。它比冒泡排序快2倍。一般不用在数据大于1000的场合下使用插入排序,或者重复排序超过200数据项的序列。
6 冒泡排序(BubbleSort)
冒泡排序是最慢的排序算法。在实际运用中它是效率最低的算法。它通过一趟又一趟地比较数组中的每一个元素,使较大的数据下沉,较小的数据上升。它是O(n^2)的算法。
7
交换排序(ExchangeSort)和选择排序(SelectSort)
这两种排序方法都是交换方法的排序算法,效率都是 O(n2)。在实际应用中处于和冒泡排序基本相同的地位。它们只是排序算法发展的初级阶段,在实际中使用较少。
8
基数排序(RadixSort)
基数排序和通常的排序算法并不走同样的路线。它是一种比较新颖的算法,但是它只能用于整数的排序,如果我们要把同样的办法运用到浮点数上,我们必须了解浮点数的存储格式,并通过特殊的方式将浮点数映射到整数上,然后再映射回去,这是非常麻烦的事情,因此,它的使用同样也不多。而且,最重要的是,这样算法也需要较多的存储空间。
9 总结
下面是一个总的表格,大致总结了我们常见的所有的排序算法的特点。
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) |
B是真数(0-9), R是基数(个十百) |
| Shell | O(nlogn) | O(ns) 1<s<2 | 不稳定 | O(1) | s是所选分组 |
| 快速 | O(nlogn) | O(n2) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |