一行N个方格,开始每个格子里都有一个整数。现在动态地提出一些问题和修改:提问的形式是求某一个特定的子区间[a,b]中所有元素的和;修改的规则是指定某一个格子x,加上或者减去一个特定的值A。现在要求你能对每个提问作出正确的回答。1≤N<100000,,提问和修改的总数m<10000条。
输入文件第一行为一个整数N,接下来是n行n个整数,表示格子中原来的整数。接下一个正整数m,再接下来有m行,表示m个询问,第一个整数表示询问代号,询问代号1表示增加,后面的两个数x和A表示给位置X上的数值增加A,询问代号2表示区间求和,后面两个整数表示a和b,表示要求[a,b]之间的区间和。
共m行,每个整数
6
4
5
6
2
1
3
4
1 3 5
2 1 4
1 1 9
2 2 6
22
22
1≤N≤100000, m≤10000 。
分类标签 Tags 点此展开
代码
#include<cstdio> #include<cstdlib> #include<iostream> #include<cstring> #include<algorithm> #include<vector> #define MAXN 101000 #define MAXT MAXN*4 #define lch now<<1 #define rch ((now<<1)+1) #define smid ((l+r)>>1) int a[MAXN]; using namespace std; struct node { int sum; int l,r; }sgt[MAXT]; int read(){ register int f=1,x=0; register char ch=getchar(); while(ch>'9'||ch<'0'){if(ch=='-') f=-1;ch=getchar();} while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar(); return x*f; } void build(int now,int l,int r){ sgt[now].l=l; sgt[now].r=r; if(l==r) {sgt[now].sum=a[l];return;} build(lch,l,smid); build(rch,smid+1,r); sgt[now].sum=sgt[lch].sum+sgt[rch].sum; } void modify(int now,int pos,int l,int r,int v){ if(l==r){ sgt[now].sum+=v;return; } if(pos<=smid) modify(lch,pos,l,smid,v); else modify(rch,pos,smid+1,r,v); sgt[now].sum=sgt[lch].sum+sgt[rch].sum; } int query(int now,int l,int r,int x,int y){ if(l==x&&r==y) return sgt[now].sum; if(y<=smid) return query(lch,l,smid,x,y); else if(smid<x) return query(rch,smid+1,r,x,y); else return query(lch,l,smid,x,smid)+query(rch,smid+1,r,smid+1,y); } int main(){ int n=read(); for(int i=1;i<=n;i++) a[i]=read(); build(1,1,n); int m=read(); for(int i=1;i<=m;i++){ int opt=read(); if(opt==1){ int pos=read(),v=read(); modify(1,pos,1,n,v); }else{ int x=read(),y=read(); printf("%d ",query(1,1,n,x,y)); } } return 0; }
更新一下代码风格
#include<bits/stdc++.h> using namespace std; #define N 100010 #define lc k<<1 #define rc k<<1|1 #define mid (l+r>>1) int tmp[N],a[N<<2]; void build(int k,int l,int r){ if(l==r){ a[k]=tmp[l];return ; } build(lc,l,mid); build(rc,mid+1,r); a[k]=a[lc]+a[rc]; } void add(int k,int l,int r,int pos,int y){ if(l==r){ a[k]+=y;return ; } if(pos<=mid) add(lc,l,mid,pos,y); else add(rc,mid+1,r,pos,y); a[k]=a[lc]+a[rc]; } int query(int k,int l,int r,int x,int y){ if(l==x&&r==y) return a[k]; if(y<=mid) return query(lc,l,mid,x,y); else if(x>mid) return query(rc,mid+1,r,x,y); else return query(lc,l,mid,x,mid)+query(rc,mid+1,r,mid+1,y); } int main(){ int n,m,opt,x,y; scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",tmp+i); build(1,1,n); scanf("%d",&m); for(int i=1;i<=m;i++){ scanf("%d%d%d",&opt,&x,&y); if(opt==1) add(1,1,n,x,y); else printf("%d ",query(1,1,n,x,y)); } return 0; }
树状数组版
#include<bits/stdc++.h> using namespace std; #define N 100010 int n,m,opt,x,y,c[N]; int lowbit(int x){ return x&-x; } void updata(int p,int v){ for(int i=p;i<=n;i+=lowbit(i)) c[i]+=v; } int query(int p){ int ans=0; for(int i=p;i>=1;i-=lowbit(i)) ans+=c[i]; return ans; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++) scanf("%d",&x),updata(i,x);//初始化树状数组 scanf("%d",&m); for(int i=1;i<=m;i++){ scanf("%d%d%d",&opt,&x,&y); if(opt==1) updata(x,y); else printf("%d ",query(y)-query(x-1));//类似一个前缀和 } return 0; }
-----------------------------------------------------------------------------------------------------------------------------------------------
华丽的分割线
------------------------------------------------------------------------------------------------------------------------------------------------
ps:补一下树状数组
如果给定一个数组,要你求里面所有数的和,一般都会想到累加。但是当那个数组很大的时候,累加就显得太耗时了,时间复杂度为O(n),并且采用累加的方法还有一个局限,那就是,当修改掉数组中的元素后,仍然要你求数组中某段元素的和,就显得麻烦了。所以我们就要用到树状数组,他的时间复杂度为O(lgn),相比之下就快得多。下面就讲一下什么是树状数组:
一般讲到树状数组都会少不了下面这个图:
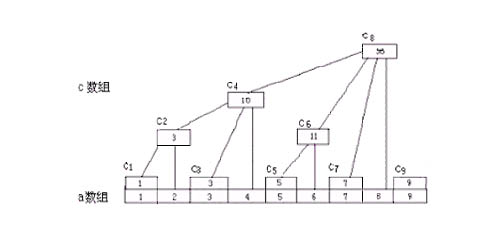
下面来分析一下上面那个图看能得出什么规律:
据图可知:c1=a1,c2=a1+a2,c3=a3,c4=a1+a2+a3+a4,c5=a5,c6=a5+a6,c7=a7,c8=a1+a2+a3+a4+a5+a6+a7+a8,c9=a9,c10=a9+a10,c11=a11........c16=a1+a2+a3+a4+a5+.......+a16。
分析上面的几组式子可知,当 i 为奇数时,ci=ai ;当 i 为偶数时,就要看 i 的因子中最多有二的多少次幂,例如,6 的因子中有 2 的一次幂,等于 2 ,所以 c6=a5+a6(由六向前数两个数的和),4 的因子中有 2 的两次幂,等于 4 ,所以 c4=a1+a2+a3+a4(由四向前数四个数的和)。
(一)有公式:cn=a(n-a^k+1)+.........+an(其中 k 为 n 的二进制表示中从右往左数的 0 的个数)。
那么,如何求 a^k 呢?求法如下:
int lowbit(int x){ return x&-x; }
lowbit()的返回值就是 2^k 次方的值。
求出来 2^k 之后,数组 c 的值就都出来了,接下来我们要求数组中所有元素的和。
(二)求数组的和的算法如下:
(1)首先,令sum=0,转向第二步;
(2)接下来判断,如果 n>0 的话,就令sum=sum+cn转向第三步,否则的话,终止算法,返回 sum 的值;
(3)n=n - lowbit(n)(将n的二进制表示的最后一个零删掉),回第二步。
代码实现:
int query(int p){ int ans=0; for(int i=p;i>=1;i-=lowbit(i)) ans+=c[i]; return ans; }
(三)当数组中的元素有变更时,树状数组就发挥它的优势了,算法如下(修改为给某个节点 i 加上 x ):
(1)当 i<=n 时,执行下一步;否则的话,算法结束;
(2)ci=ci+x ,i=i+lowbit(i)(在 i 的二进制表示的最后加零),返回第一步。
代码实现:
void updata(int p,int v){ for(int i=p;i<=n;i+=lowbit(i)) c[i]+=v; }