题目描述
设计一个找到数据流中第K大元素的类(class)。注意是排序后的第K大元素,不是第K个不同的元素。
你的 KthLargest 类需要一个同时接收整数 k 和整数数组nums 的构造器,它包含数据流中的初始元素。每次调用 KthLargest.add,返回当前数据流中第K大的元素。
示例
int k = 3;
int[] arr = [4,5,8,2];
KthLargest kthLargest = new KthLargest(3, arr);
kthLargest.add(3); // returns 4
kthLargest.add(5); // returns 5
kthLargest.add(10); // returns 5
kthLargest.add(9); // returns 8
kthLargest.add(4); // returns 8
说明
你可以假设 nums 的长度≥ k-1 且k ≥ 1。
算法
当提到排序后的第K大元素或者排序后的最K小元素时,并且经常伴随着数据的插入或弹出时,应该能想到利用堆这种数据结构。
本题的算法思路为:
- 目标:在KthLargest这个类中维护一个最小堆,且保证堆的大小为k。
- 初始时,堆中元素还不满k个时,我们一边将元素插入最末尾,然后一边调整堆为最小堆。
- 当堆中元素已满k个时,再有新的元素要往堆里放的时候,我们将它与堆顶作比较。如果待放入的值比堆顶大,我们将待放入的值放在堆顶,然后重新调整最小堆;如果待放入的值小于或者等于堆顶的值,就什么也不做。
- 结果:我们会惊奇地发现,堆顶存放的数就是要求的数据流中第K大元素,将其返回即可。
为了更好的示意整个过程,我将以题目描述中给的例子为例,在图上画出具体的过程:
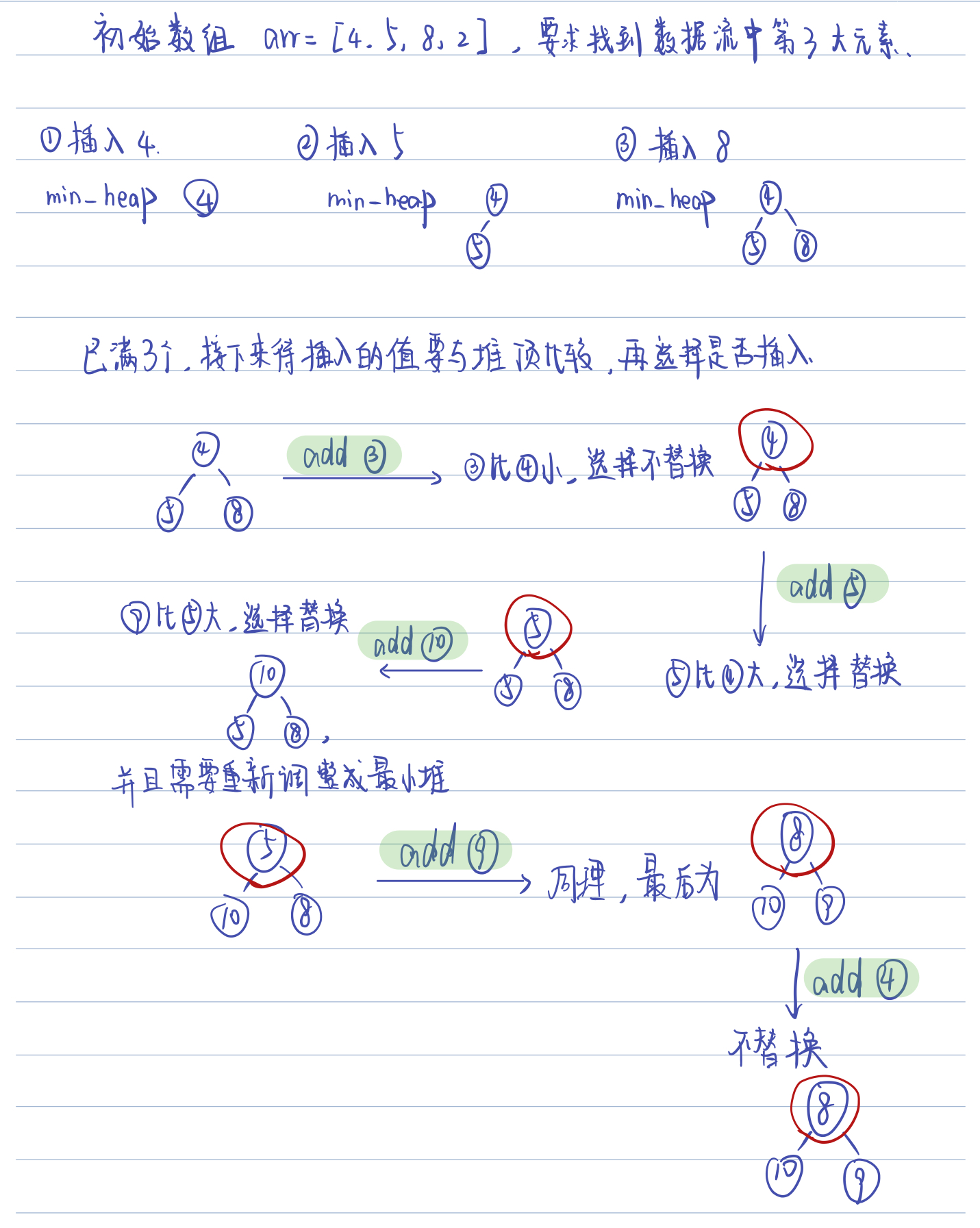
边界条件
当然,本题的边界条件就是考虑k的值和堆中元素的个数。
代码
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
class KthLargest {
public:
vector<int> min_heap;
int _k;
KthLargest(int k, vector<int> nums) {
_k = k;
for(int i = 0; i < _k && i < nums.size(); i++)
{
min_heap.push_back(nums[i]);
PercUp(i);
}
for (int i = _k; i < nums.size(); i++)
adjust(nums[i]);
}
int add(int val) {
// 边界条件,即堆中还未满k个元素
if (min_heap.size() < _k)
{
min_heap.push_back(val);
PercUp(min_heap.size()-1);
}
else
adjust(val);
return min_heap[0];
}
void adjust(int x)
{
/*** 本函数用于比较待插入的元素x与堆顶的值大小,以便确认是否替换堆顶并调整最小堆 ***/
// 堆顶元素更大,直接返回
if (x <= min_heap[0])
return;
// 替换并调整的函数接口
PercDown(x);
}
void PercUp(int p)
{
/*** 本函数意在将行插入在末尾的元素调整至合适的位置以维护整个堆是最小堆 ***/
int father, child = p;
int X = min_heap[child];
while (child != 0)
{
father = (child - 1) / 2;
// 与父节点比较
if (min_heap[father] <= X)
break;
min_heap[child] = min_heap[father];
child = father;
}
min_heap[child] = X;
}
void PercDown(int X)
{
/*** 本函数将新替换进来的堆顶元素找到一个合适的位置存放以维持整个堆是最小堆***/
int father = 0;
while (2*father+1 < _k)
{
int child = 2 * father + 1;
// 找两个字节点中比较小的那个
if (child + 1 < _k && min_heap[child] > min_heap[child+1])
child++;
// 与子节点比较
if (min_heap[child] >= X)
break;
min_heap[father] = min_heap[child];
father = child;
}
min_heap[father] = X;
}
};
int main()
{
vector<int> nums = {4, 5, 8, 2};
KthLargest kth(3, nums);
cout << kth.add(3) << endl; // returns 4
cout << kth.add(5) << endl; // returns 5
cout << kth.add(10) << endl; // returns 5
cout << kth.add(9) << endl; // returns 8
cout << kth.add(4) << endl; // returns 8
return 0;
}
最后
其实c++中的stl有定义一个容器-优先队列,它的本质是堆实现的。直接利用容器的话,也不用自己写堆的调整算法了,但是堆排序作为一个比较基础的排序算法,多写几遍掌握原理还是比较有益处的。堆排序的调整算法在另一篇博文https://www.cnblogs.com/shayue/p/10426127.html中。