72. 编辑距离

题目描述

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

示例1

输入: word1 = "horse", word2 = "ros"
输出: 3
解释:

horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例2

输入: word1 = "intention", word2 = "execution"
输出: 5
解释:

intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

题意表述

由题意可得这题应该是用动态规划解决，别问我为啥看的出来。。。我也是猜的。

说到动态规划，就想到状态转移方程，说到状态转移方程，我就想到。。。嗯。。。两开花。

不对，是怎样找出状态转移方程？

做到现在，我做的动态规划题目终于一只手数不过来了，我得出的经验就是一定要动手演算，而且我接触到的题目一般就分为两种情况：
1. dp是一维的，和前几个相关
2. dp是二维的，和左、上、斜上对角3个数中的几个相关

当然，我做的题目还很少，但是就我已经得到的经验，遇到动态规划相关的题目我都会先从这些角度试试找寻规律。

算法

下面是我的演算过程：

1. 一些规定

   • 既然是字符串的变换，那么dp应该是2维的

   • 将word1置于横轴，word2置于纵轴（当然可以换过来，换过来后dp[i][j]的定义也要换）。这么一来，dp[i][j]代表的含义为word1[j]变换到word[i]需要的最少操作数。可能有些抽象，举个例子：

     word1 = "horse"，word2 = "ros"，那么二维dp数组长这样
     
        h  o  r  s  e
     r
     o        *
     s  
     
     dp[1][2]代表的含义为"hor"变换到"ro"需要的最少操作数，所以同理，dp[2][4]即为最终要求的目标值，代表"horse"变换到"ros"需要的最少操作数
     

2. 演算

   • 填充初值

     

     

     

   • 状态转移方程

     

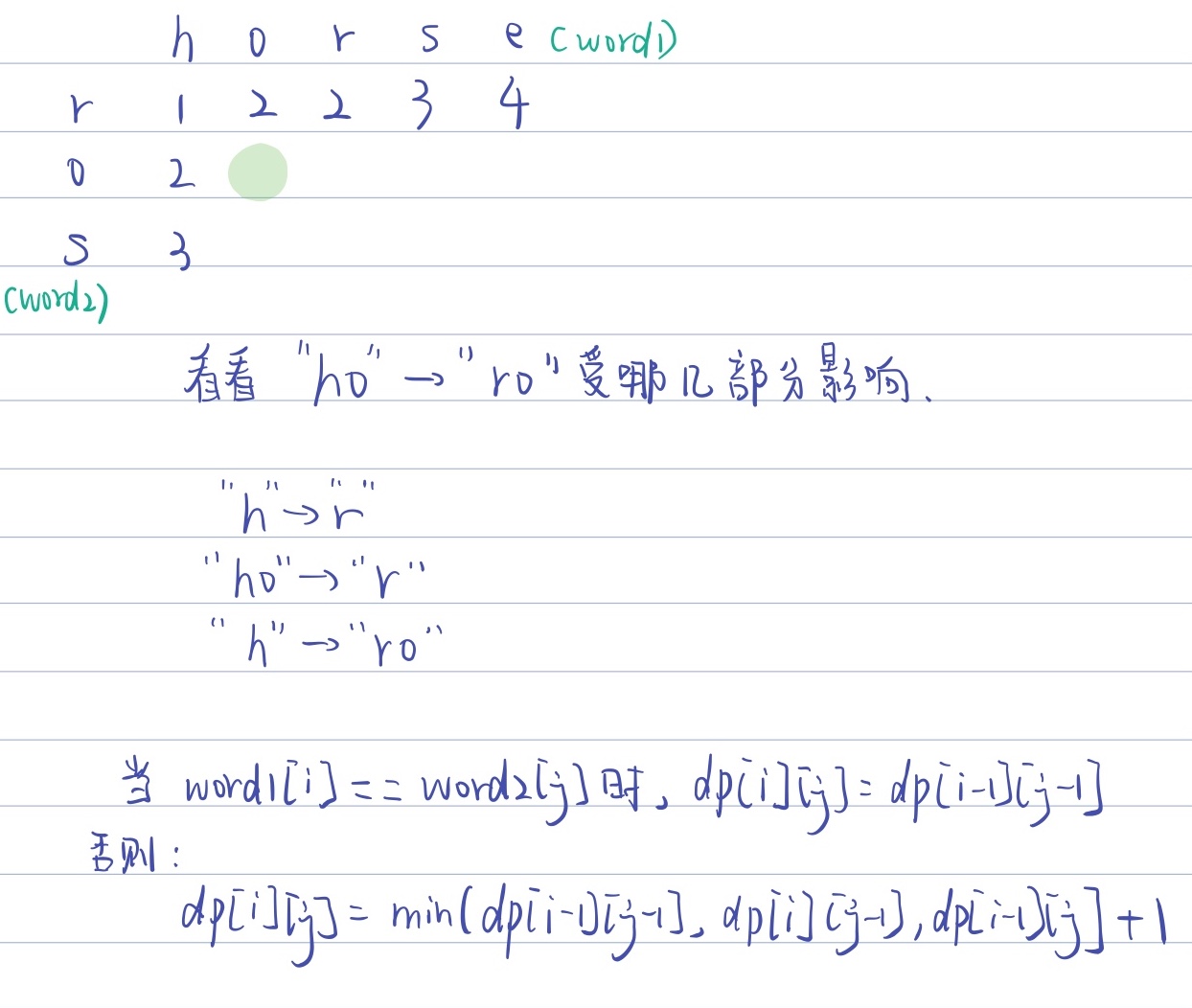
代码

#include <iostream>
#include <string>
#include <algorithm>
using namespace std;

/***
 *  状态转移方程，dp[i][j]与上、左、斜上角3个数都有关
 *  if(word1[i] == word2[j])    dp[j][i] = dp[j-1][i-1]
 *  else    dp[j][i] = min(dp[j-1][i-1], dp[j-1][i], dp[j][i-1]) + 1
 ***/

class Solution {
public:
    int minDistance(string word1, string word2) {
        // 边界条件
        if(word1 == "" && word2 == "")
            return 0;
        else if(word1 == "")
            return word2.size();
        else if(word2 == "")
            return word1.size();

        // 参数
        int col = word1.size();
        int row = word2.size();
        int dp[row][col], i, j;

        // 初始化
        word1[0] == word2[0] ? (dp[0][0] = 0) : (dp[0][0] = 1);
        bool flag = true;
        for(i = 1; i < col; i++)
        {
            if(word1[i] == word2[0])
            {
                if(flag == true)
                {
                    dp[0][i] = dp[0][i-1];
                    flag = false;
                }
                else
                    dp[0][i] = dp[0][i-1]+1;
            }
            else
                dp[0][i] = dp[0][i-1] + 1;
        }

        flag = true;
        for(j = 1; j < row; j++)
        {
            if(word2[j] == word1[0])
            {
                if(flag == true)
                {
                    dp[j][0] = dp[j-1][0];
                    flag = false;
                }
                else
                    dp[j][0] = dp[j-1][0] + 1;
            }
            else
                dp[j][0] = dp[j-1][0] + 1;
        }

        // 遍历更新dp[i][j]
        for(j = 1; j < row; j++)
        {
            for(i = 1; i < col; i++)
            {
                if(word1[i] == word2[j])   
                    dp[j][i] = dp[j-1][i-1];
                else
                    dp[j][i] = min(dp[j-1][i-1], min(dp[j-1][i], dp[j][i-1])) + 1;
            }
        }
        return dp[row-1][col-1];
    }
};

int main()
{
    string word1, word2;
    word1 = "pneumonoultramicroscopicsilicovolcanoconiosis", word2 = "ultramicroscopically";
    Solution s;
    cout << s.minDistance(word1, word2) << endl;
    return 0;
}