题目描述:
给定一个二叉搜索树,同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树,使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点,所以结果应当返回修剪好的二叉搜索树的新的根节点。
示例1:
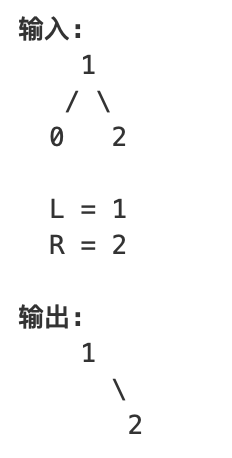
示例2:

题意:
修剪BST,使树中的结点满足值在L和R之间。
切记不可采用先序遍历,再取符合要求的值重新建树,这样会打乱原本树中某些节点的先后顺序。正解还是采用递归。
算法:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 TreeNode* trimBST(TreeNode* root, int L, int R) { 13 if(root == NULL) 14 return NULL; 15 if(root->val <= R && root->val >= L) //当前值符合要求,对左右子树修剪 16 { 17 root->left = trimBST(root->left, L, R); 18 root->right = trimBST(root->right, L, R); 19 } 20 else if(root->val > R) //如果当前值都比R大了,右边的结点值肯定比R更大,所以仅考虑左子树 21 { 22 return trimBST(root->left, L, R); 23 } 24 else if(root->val < L) //同上 25 { 26 return trimBST(root->right, L, R); 27 } 28 return root; 29 } 30 };