树上差分(LCA辅助(树上倍增版))
题面回顾
有一棵 $n$ 个节点,边权为 $1$ 的树,有 $m$ 个人在 $S[i]$ 和 $T[i]$ 之间的最短路径上从 $0$ 时刻出发开始跑步,每个节点 $i$ 上都有一个观察员,观察第 $w[i]$ 秒恰好经过该节点的人数。问:每个观察员可以看到多少人?
思路分析
(解释一波lyd大佬的思路)
由于每个人运动的路径是固定的,所以可以把每个人的路径分为两段:起点 $s$ 到 $lca$ , $lca$ 到终点 $t$
因此,对于每个观测点 $x$ ,有两种情况可以观察到第 $i$ 个人(其中 $d$ 数组表示深度,可以用bfs一遍处理倍增时进行预处理)
1. $x$ 在 $s[i]$ 到 $lca(s[i],t[i])$ 的路径上, $w[x]=d[s[i]]-d[x]$
2. $x$ 在 $lca(s[i],t[i])$ 到 $t[i]$ 的路径上, $w[x]=d[s[i]]+d[x]-2* d[lca(s[i],t[i])] $
这两种情况其实是类似的,我们不妨先来考虑第一种
移项得 $w[x]+d[x]=d[s[i]]$
这就相当于在 $s[i]$ 到 $lca(s[i],t[i])$ 的路径上每个节点放一个类型为 $d[s[i]]$ 的物品,求最终每个节点上放有多少个类型为 $d[x]+w[x]$ 的物品
这让我们想到了雨天的尾巴,但是那道线段树合并模板题是因为要求每个节点最多的种类是什么,这道题则是求给定的种类有多少个物品
因此可以不用敲线段树合并。。。
下面是做法:
1. 对每个节点建立两个 $vector$ 数组,分别表示在这个节点产生或消失的物品的类型
2. 建立全局数组 $c$ ,记录每种类型物品的数量(相当于桶)
3. 开始做dfs,当遇到一个点 $x$ 时,先保存当前 $c[w[x]+d[x]]$ 的值,记为 $cnt$
4. 然后扫描 $x$ 的两个 $vector$ ,产生数组中出现 $z$ 就让 $c[z]++$ ,消失数组中出现 $z$ 就让 $c[z]--$ 。这是因为如果这个物品在 $x$ 的子树中即产生又消失,那么对 $x$ 无影响;如果只产生不消失,说明消失的地方在 $x$ 上面,那么 $x$ 上就会放下这个物品;由于规定下产生,上消失,所以不可能出现消失了但没有产生的情况
5. 然后扫完子节点返回 $x$ ,用当前的 $c[w[x]+d[x]]$ 减去扫描前的 $c[w[x]+d[x]]$ (也就是存好的 $cnt$ ),记为 $x$ 处的 $w[x]+d[x]$ 类物品的数量
下面是几个栗子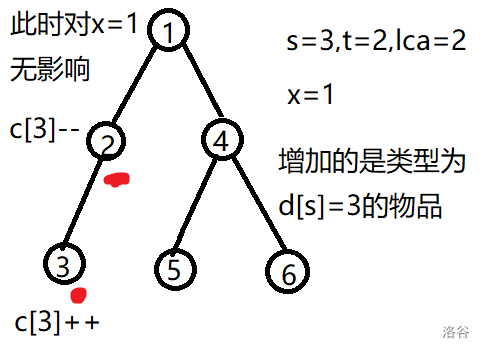
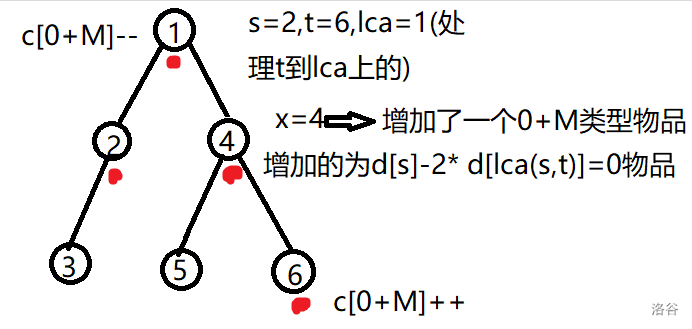
然后刚才说过的第二种情况也差不多,t[i]到 $lca$ 路径上增加的物品类型为 $d[s[i]]-2* d[lca(s[i],t[i])]$ , 最后统计每个结点 $x$ 处物品 $w[x]-d[x]$ 的数量
最后就可以上代码了(一些细节会在代码里讲)
代码来了
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define fr(i,a,b) for(int i=a;i<=b;i++)
#define fo(i,a,b) for(int i=a;i>=b;i--)//个人习惯而已,别太在意
#pragma GCC optimize(2)
const int M=300005;
int n,m,v[M],p,f[M][20],s[M],t[M],lca[M],w[M],c1[2*M],c2[2*M],ans[M],d[M];
int head[M],Next[2*M],ver[2*M],tot;
vector<int> ap1[M],dap1[M],ap2[M],dap2[M];
//ap即appear出现,dap即disappear消失,1和2分别是从s到lca和t到lca
queue<int> q;
void add(int x,int y) {
Next[++tot]=head[x],head[x]=tot,ver[tot]=y;
}
void bfs() {
q.push(1); d[1]=1;
while(q.size()) {
int x=q.front(); q.pop();
for(int i=head[x];i;i=Next[i]) {
int y=ver[i];
if(d[y]) continue;
d[y]=d[x]+1;
f[y][0]=x;
fr(j,1,p) f[y][j]=f[f[y][j-1]][j-1];
//LCA的倍增预处理(这个不用我多说了吧)
q.push(y);
}
}
}
int LCA(int x,int y) {
if(d[x]>d[y]) swap(x,y);
fo(i,p,0) if(d[f[y][i]]>=d[x]) y=f[y][i];
if(x==y) return x;
fo(i,p,0) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
void dfs(int x) {
v[x]=1;
int cnt1=c1[w[x]+d[x]],cnt2=c2[w[x]-d[x]+M];
//cnt2加这个M是因为w[x]-d[x]有可能是负的,要加偏移值或离散化
//先保存好扫描前的数量
for(int i=0;i<ap1[x].size();i++) c1[ap1[x][i]]++;
for(int i=0;i<dap1[x].size();i++) c1[dap1[x][i]]--;
for(int i=0;i<ap2[x].size();i++) c2[ap2[x][i]+M]++;
//当然后面的也要加偏移值
for(int i=0;i<dap2[x].size();i++) c2[dap2[x][i]+M]--;
//其实就是个差分吧
for(int i=head[x];i;i=Next[i]) {
int y=ver[i];
if(v[y]) continue;
dfs(y);
}
ans[x]=c1[w[x]+d[x]]-cnt1+c2[w[x]-d[x]+M]-cnt2;
//相减即为答案
//容易发现从两个端点到lca是互不干扰的
}
int main(){
std::ios::sync_with_stdio(false);
scanf("%d%d",&n,&m);
p=(int)log(n)/log(2)+1;
fr(i,1,n-1) {
int x,y;
scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
bfs();
fr(i,1,n) scanf("%d",&w[i]);
fr(i,1,m) {
int s,t;
scanf("%d%d",&s,&t);
int lca=LCA(s,t);
ap1[s].push_back(d[s]);
dap1[f[lca][0]].push_back(d[s]);
ap2[t].push_back(d[s]-2*d[lca]);
dap2[lca].push_back(d[s]-2*d[lca]);
//记录物品出现和消失的类型
}
dfs(1);
fr(i,1,n) printf("%d ",ans[i]);
return 0;
}