这个题看似很简单:
题目:
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
当看到这个题目得到时候,我的第一反应是:考虑矩阵为空,只有一行,只有一列,以及一般情况m×n矩阵。这个思维很重要,让我们无法忽视很多的边界问题。!!!以后但凡是矩阵问题,首先需要考虑特殊矩阵。
其次,我将这个问题看作是一个剥洋葱的问题。即按照这个思路打印:打印一圈,再打印一圈,再打印一圈,直到打印到最内圈。完毕!我先给出一个完整的通过检测的代码:
1 class Solution { 2 public: 3 vector<int> printMatrix(vector<vector<int> > matrix) { 4 const int Row = matrix.size(); 5 const int Col = matrix[0].size(); 6 vector<int> res; 7 if(Row|| Col) 8 { 9 if(Row == 1) 10 for(int i = 0;i<Col;i++) 11 res.push_back(matrix[0][i]); 12 else if(Col ==1) 13 for(int i = 0;i<Row;i++) 14 res.push_back(matrix[i][0]); 15 else{ 16 int index_row =0; 17 int index_col =0; 18 int start_row = 0; 19 int start_col = 0; 20 while((start_row <=(Row-1)/2) && (start_col<=(Col-1)/2))//??? 21 { 22 while(index_col <= Col-1-start_col) 23 { 24 res.push_back(matrix[index_row][index_col]); 25 index_col++; 26 } 27 index_col--; 28 index_row++; 29 while(index_row <= Row-1-start_row) 30 { 31 res.push_back(matrix[index_row][index_col]); 32 index_row++; 33 } 34 index_row--; 35 index_col--; 36 while(index_col >=start_col && index_row != start_row) 37 { 38 res.push_back(matrix[index_row][index_col]); 39 index_col--; 40 } 41 index_col++; 42 index_row--; 43 while(index_row >start_row ) 44 { 45 res.push_back(matrix[index_row][index_col]); 46 index_row--; 47 } 48 start_row++; 49 start_col++; 50 index_row = start_row; 51 index_col = start_col; 52 } 53 } 54 return res; 55 } 56 } 57 };
下面我来画一下这个图: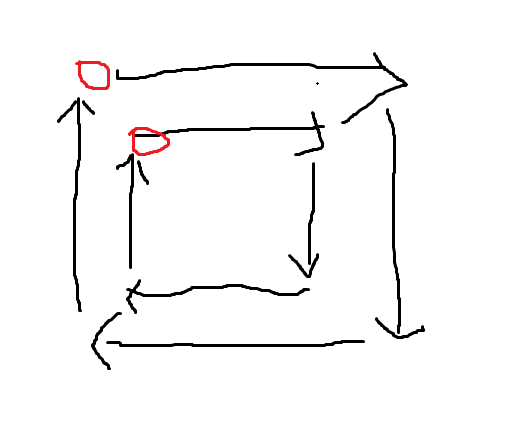
也就是我们按照图示打印所有的矩阵元素,我们没有任何技巧的情况下,所能想到的方法就是,从图中红色标记点开始,执行四趟循环,打印完四个路径。这个大思路总体是没有错误的。我们来看看这其中要注意什么问题:
问题1:从哪里开始?也就是图中红色的地方,那么红色的地方索引是多少呢?
问题2:到哪里结束?也就是最后一次执行完是什么时候,即外层的大循环执行次数怎么决定?
问题3:我们在打印的时候,四个角的位置,既属于这一行,也属于这一列,我们如何避免重复打印?
问题4:我们如何标记索引让下一次的行减少两行,列减少两列?
考虑完上述四个问题:
我之前给出了如下代码:
1 class Solution { 2 public: 3 vector<int> printMatrix(vector<vector<int> > matrix) { 4 const int Row = matrix.size(); 5 const int Col = matrix[0].size(); 6 vector<int> res; 7 if(Row|| Col) 8 { 9 if(Row == 1) 10 for(int i = 0;i<Col;i++) 11 res.push_back(matrix[0][i]); 12 else if(Col ==1) 13 for(int i = 0;i<Row;i++) 14 res.push_back(matrix[i][0]); 15 else{ 16 int index_row =0; 17 int index_col =0; 18 int start_row = 0; 19 int start_col = 0; 20 while((start_row <=(Row-1)/2) && (start_col<=(Col-1)/2))//??? 21 { 22 while(index_col <= Col-1-start_col) 23 { 24 res.push_back(matrix[index_row][index_col]); 25 index_col++; 26 } 27 index_col--; 28 index_row++; 29 while(index_row <= Row-1-start_row) 30 { 31 res.push_back(matrix[index_row][index_col]); 32 index_row++; 33 } 34 index_row--; 35 index_col--; 36 while(index_col >=start_col ) 37 { 38 res.push_back(matrix[index_row][index_col]); 39 index_col--; 40 } 41 index_col++; 42 index_row--; 43 while(index_row >start_row ) 44 { 45 res.push_back(matrix[index_row][index_col]); 46 index_row--; 47 } 48 start_row++; 49 start_col++; 50 index_row = start_row; 51 index_col = start_col; 52 } 53 } 54 return res; 55 } 56 } 57 };
代码看似没啥差别,请注意第36行代码的变换,我们来看一下通过率:
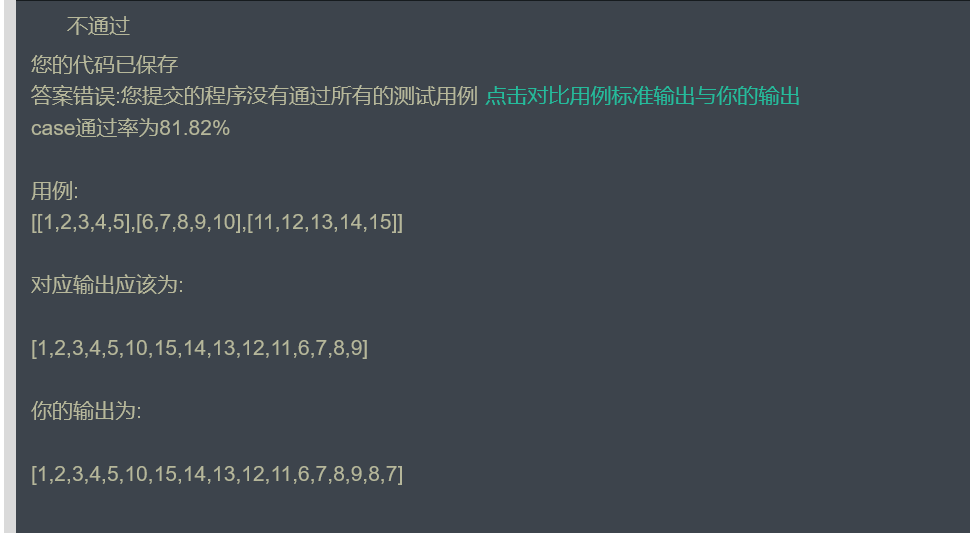
可以看到,大部分输出都是正确的,只有后面有一些错误输出,主要原因是:我们上述代码并不适应最内层只剩一行或者只剩一列的情况。因此,我们加上了:
1 index_row != start_row
也就是避免重复打印同一行或者同一列,当然,这种情况通常也只会在最内层循环产生。
再来关注的一个问题是:如何让每层洋葱循环的行和列依次减去2? 我们发现:0+4 = 1+3=row,这么说你懂了吧。
最后的一个问题是:最后一个红色开始在哪?很明显,外层循环已经给出了答案。