EM 算法是一种迭代算法,1977 年由 Dempster 等人总结提出,用于含隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计。EM 算法的每次迭代由两步组成:E 步,求期望(expectation); M 步,求极大(maximization)。所以这一算法称为期望极大算法(expectation maximization algorithm),简称 EM 算法。
1 EM 算法
1.1 预备知识
(1) 观测变量和隐变量
概率模型有时候既含有观测变量(observable variable),又含有隐变量或潜在变量(latent variable)。如果概率模型的变量都是观测变量,那么给定数据,可以直接用极大似然估计法,或贝叶斯估计法估计模型参数。但是,当模型含有隐变量时,就不能简单地使用这些估计方法。
(2)完全数据和不完全数据
用 (Y) 表示观测随机变量的数据,(Z) 表示隐随机变量的数据。(Y) 和 (Z) 连在一起成为完全数据(complete-data),观测数据 (Y) 又称为不完全数据(incomplete-data)。假设给定观测数据 (Y),其概率分布是 (P(Y| heta)),其中 ( heta) 是需要估计的模型参数,那么不完全数据 (Y) 的似然函数是 (P(Y| heta)),对数似然函数 (L( heta) = log P(Y| heta));假设 (Y) 和 (Z) 的联合概率分布是 (P(Y, Z| heta)),那么完全数据的对数似然函数是 (log P(Y, Z| heta))。EM 算法通过迭代求 (L( heta) = log P(Y| heta)) 的极大似然估计。每次迭代包含两步:E 步:求期望;M 步,求极大化。
(3)Jensen 不等式
当 (f(x)) 为凸函数(这里指下凸函数,有的教材凹凸的定义不同)时,有Jensen 不等式(也称詹森不等式、琴生不等式),
可以作一个很直观的解释(如下图),比如说在二维空间上,凸函数是一个开口向上的抛物线,假如我们有两个点 (a, b),那么 (f(E[x])) 表示的是两个点的均值的纵坐标,而 (E[f(x)]) 表示的是两个点纵坐标的均值。
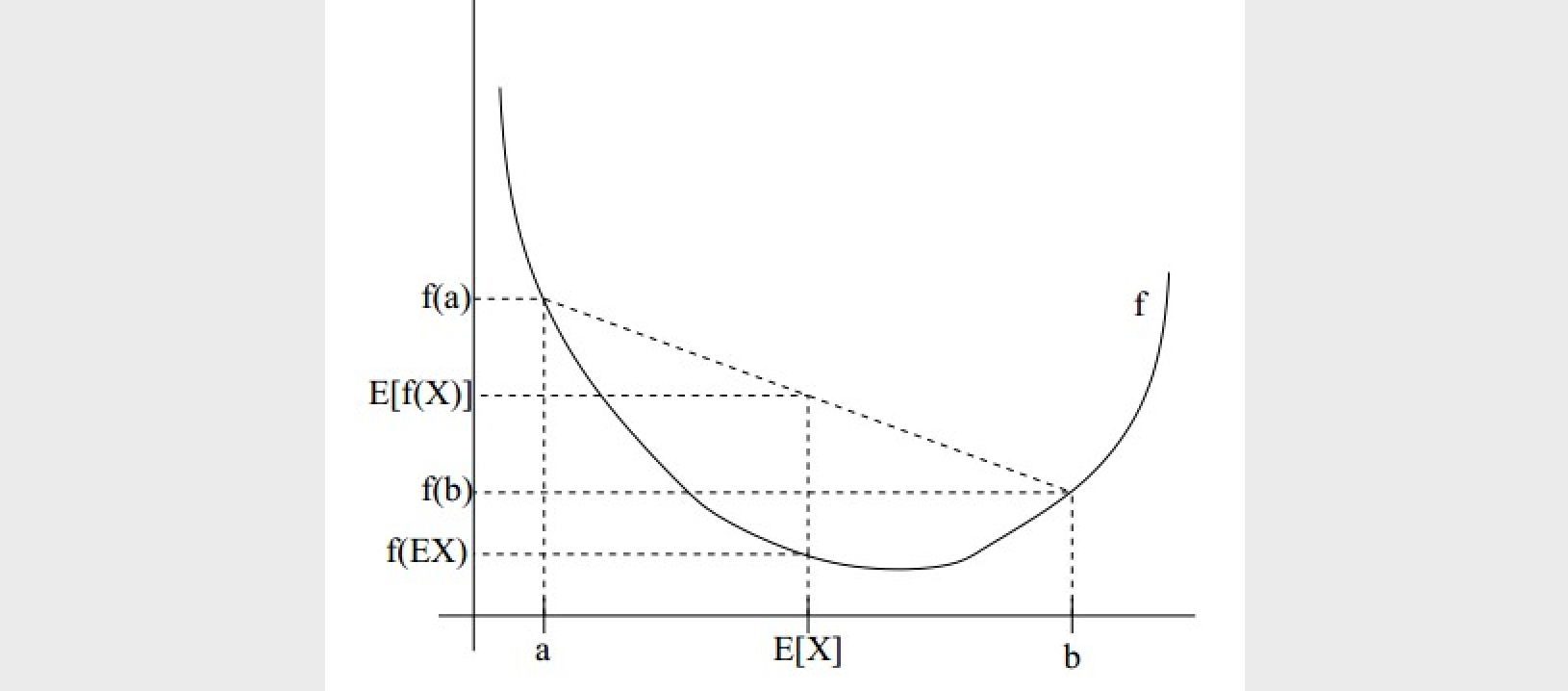
当函数 (f(x)) 为对数函数((log),为凹函数,或上凸函数)时,上面的公式刚好反过来,即
1.2 EM 算法的引入
例(三硬币模型) (quad) 假设有 3 枚硬币,分别记作 (A, B, C)。这些硬币正面出现的概率分别是 (pi, p, q)。进行如下掷硬币实验:先掷硬币 (A),根据其结果选出硬币 (B) 或硬币 (C),正面选硬币 (B),反面选硬币 (C);然后掷选出的硬币,掷硬币的结果,出现正面记作 1,出现反面记作 0;独立地重复 (n) 次试验(这里,(n=10)),观测结果如下:
假设只能观测到掷硬币的结果,不能观测掷硬币的过程。问如何估计三硬币正面出现的概率,即三硬币模型的参数(((pi, p, q)))。
解 (quad) 三硬币模型可以写作
这里,随机变量 (y) 是观测变量,表示一次试验观测的结果是 1 或 0;随机变量 (z) 是隐变量,表示未观测到的掷硬币 (A) 的结果(正面或反面);( heta = (pi, p, q)) 是模型参数。这一模型是以上数据的生成模型。注意,随机变量 (y) 的数据可以观测,随机变量 (z) 的数据不可观测。
将观测数据表示为 (Y=(Y_1, Y_2, cdots, Y_n)^T),未观测数据表示为 (Z=(Z_1, Z_2, cdots, Z_n)^T),则观测数据的似然函数为
即
考虑求模型参数 ( heta = (pi, p, q)) 的极大似然估计,即
这个问题没有解析解,只有通过迭代的方法求解。EM 算法就是可以用于求解这个问题的一种迭代算法。
1.3 算法(EM 算法)
EM 算法
输入:观测变量数据 (Y),隐变量数据 (Z),联合分布 (P(Y, Z| heta)),条件分布 (P(Z|Y, heta));
输出:模型参数 ( heta)。
(1)选择参数初值 ( heta^{(0)}),开始迭代;
(2)E 步:记 ( heta^{(i)}) 为第 (i) 次迭代参数 ( heta) 的估计值,在第 (i+1) 次迭代的 (E) 步,计算
这里,(P(Z|Y, heta^{(i)})) 是在给定观测数据 (Y) 和当前的参数估计 ( heta^{(i)}) 下隐变量数据 (Z) 的条件概率分布;
(3)M 步:求使 (Q( heta, heta^{(i)})) 极大化的 ( heta),确定第 (i+1) 次迭代的参数的估计值 ( heta^{(i+1)})
(4)重复第(2)和第(3)步,直到收敛。
上式的函数 (Q( heta, heta^{(i)})) 是 EM 算法的核心,称为 (Q) 函数((Q) function)。
定义(Q 函数) (quad) 完全数据的对数似然函数 (log P(Y, Z| heta)) 关于在给定观测数据 (Y) 和当前参数 ( heta^{(i)}) 下对未观测数据 (Z) 的条件概率分布 (P(Z|Y, heta^{(i)})) 的期望称为 (Q) 函数,即
下面对 EM 算法作几点说明:
步骤(1):参数的初值可以任意选择,但需注意 EM 算法对初值是敏感的。
步骤(2):E 步求 (Q( heta, heta^{(i)})) 。(Q) 函数式中 (Z) 是未观测数据,(Y) 是观测数据。注意,(Q( heta, heta^{(i)})) 的第 1 个变元表示要极大化的参数,第 2 个变元表示参数的当前估计值。每次迭代实际在求 (Q) 函数及其极大。
步骤(3):M 步求 (Q( heta, heta^{(i)})) 的极大化,得到 ( heta^{(i+1)}),完成一次迭代 ( heta^{(i)}
ightarrow heta^{(i+1)})。后面将证明每次迭代使似然函数增大或达到局部极值。
步骤(4):给出停止迭代的条件,一般是对较小的 (epsilon_1, epsilon_2),若满足
则停止迭代。
1.4 EM 算法的导出((Q( heta, heta^{(i)})) 函数的由来)
面对一个含有隐变量的概率模型,目标是极大化观测数据(不完全数据)(Y) 关于参数 ( heta) 的对数似然函数,即极大化
这一极大化的主要困难是上式中有未观测数据并有包含和(或积分)的对数。
事实上,EM 算法是通过迭代逐步近似极大化 (L( heta)) 的。假设在第 (i) 次迭代后 ( heta) 的估计值是 ( heta^{(i)})。我们希望新估计值 ( heta) 能使 (L( heta)) 增加,即 (L( heta) > L( heta^{(i)})),并逐步达到极大值。为此,考虑两者的差:
利用 Jensen 不等式(Jensen inequality)得到其下界:
令
则
即函数 (B( heta, heta^{(i)})) 是 (L( heta)) 的一个下界,而且由上式可知,
因此,任何可以使 (B( heta, heta^{(i)})) 增大的 ( heta),也可以使 (L( heta)) 增大。为了使 (L( heta)) 有尽可能大的增长,选择 ( heta^{(i+1)}) 使 (B( heta, heta^{(i)})) 达到极大,即
假设当前对于 (L( heta)) 中参数 ( heta) 的取值为 ( heta^{(i)}),求得 ( heta^{(i+1)}) 后,有
可见,(L( heta)) 确实是在逐步增大。
现在求 ( heta^{(i+1)}) 的表达式,省去对 ( heta) 的极大化而言是常数的项,有
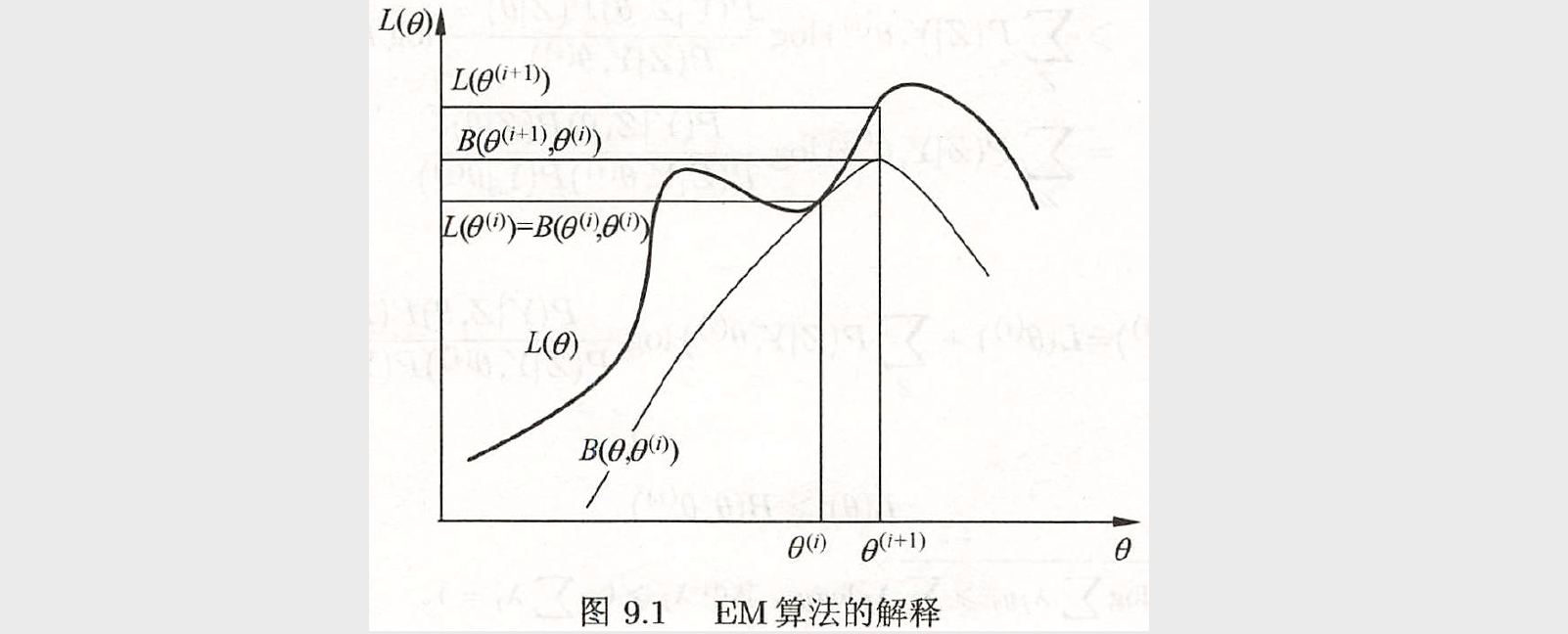
下图给出 EM 算法的直观解释,(B( heta, heta^{(i)})) 为对数似然函数 (L( heta)) 的下界。两个函数在点 ( heta = heta^{(i)}) 处相等。由上面的式子,EM 算法找到下一个点 ( heta^{(i+1)}) 使函数 (B( heta, heta^{(i)})) 极大化,也是函数 (Q( heta, heta^{(i)})) 极大化。这时由于 (L( heta) ge B( heta, heta^{(i)})),函数 (B( heta, heta^{(i)})) 的增加,保证对数似然函数 (L( heta)) 在每次迭代中也是增加的。EM 算法在点 ( heta^{(i+1)}) 重新计算 (Q) 函数值,进行下一次迭代。在这个过程中,对数似然函数 (L( heta)) 不断增大。从图可以推断出 EM 算法不能保证找到全局最优值。
2 高斯混合模型(Gaussian mixture model, GMM)
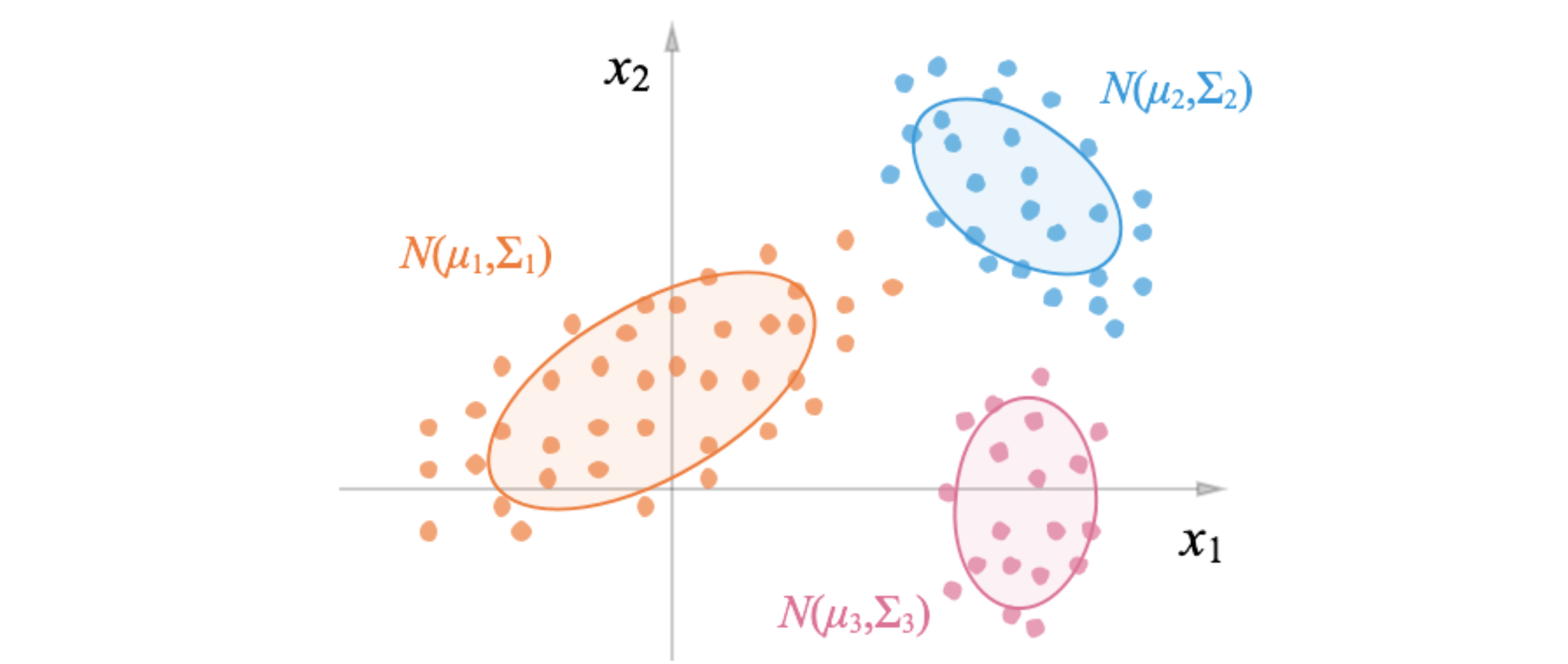
高斯混合模型是一种常见的聚类算法,EM 算法的一个重要应用是高斯混合模型的参数估计。
2.1 高斯混合模型定义
定义(高斯混合模型) (quad) 高斯混合模型是指具有如下形式的概率分布模型:
其中,(alpha_k ge 0),(sum_{k=1}^{K} alpha_k = 1);(phi(y| heta_k)) 是高斯分布密度,( heta_k = (mu_k, sigma_k^2)),
称为第 (k) 个分模型。
一般混合模型可以由任意概率分布密度函数代替高斯分布密度函数。
2.2 高斯混合模型参数估计的 EM 算法
假设观测数据 (y_1, y_2, cdots, y_N) 由高斯混合模型生成,
其中,( heta = (alpha_1, alpha_2, cdots, alpha_K; heta_1, heta_2, cdots, heta_K))。下面我们用 EM 算法估计高斯混合模型的参数 ( heta)。
1. 明确隐变量,写出完全数据的对数似然函数
可以设想观测数据 (y_j, j=1, 2, cdots, N,) 是这样产生的:(1)首先依概率 (alpha_k) 随机选择第 (k) 个高斯分布模型 (phi(y| heta_k)),(2)然后依第 (k) 个分模型的概率分布 (phi(y| heta_k)) 生成观测数据 (y_j)。
这时观测数据 (y_j, j=1, 2, cdots, N) 是已知的;反映观测数据 (y_j) 来自第 (k) 个分模型的数据是未知的,(k=1, 2, cdots, K),以隐变量 (gamma_{jk}) 表示,其定义如下:
(j=1, 2, cdots, N; k = 1, 2, cdots, K),(gamma_{jk}) 是 0-1 随机变量。
有了观测数据 (y_j) 及未观测数据 (gamma_{jk}),那么完整数据是
于是可以写出完全数据的似然函数,一组完全数据 ((y_j, gamma_{j1}, gamma_{j2}, cdots, gamma_{jK})) 的似然函数为
整个完全数据集 ((y, gamma)) 的似然函数为
那么完全数据的对数似然函数为
2. EM 算法的 E 步:确定 (Q) 函数
定义(响应度) (quad) 计算 (E(gamma_{jk} | y, heta)),记为 (hat{gamma}_{jk})
(hat{gamma}_{jk}) 是在当前模型参数下第 (j) 个观测数据来自第 (k) 个分模型的概率,称为分模型 (k) 对观测数据 (y_j) 的响应度。
将 (hat{gamma}_{jk}) 带入上面 (Q( heta, heta^{(i)})),即得
3. 确定 EM 算法的 M 步
迭代的 M 步是求函数 (Q( heta, heta^{(i)})) 对 ( heta) 的极大值,即求新一轮迭代的模型参数:
用 (hat{mu}_k, hat{sigma}_k) 及 (hat{alpha}_k, k = 1, 2, cdots, K),表示 ( heta^{(i+1)}) 的各参数,在求解过程中,同时需要满足 (sum_{k=1}^{K} alpha_k = 1),于是有:
采用拉格朗日乘子法,有
对 (mu_k, sigma_k^2) 和 (alpha_k) 求偏导数并令其为 0,得
参数 (hat{alpha}_k) 的详细推导:
[frac{partial{L( heta)}}{partial{alpha_k}} = frac{sum_{j=1}^{N} hat{gamma}_{jk}}{alpha_k} + lambda = 0 ]于是有
[sum_{j=1}^{N} hat{gamma}_{jk} + lambda alpha_k = 0 ]等式两边同时对 (k) 求和
[sum_{k=1}^{K}sum limits_{j=1}^{N} hat{gamma}_{jk} + lambda sum_{k=1}^{K}alpha_k = 0 ]得
[N + lambda = 0 ]因此有
[hat{alpha}_k = frac{sum limits_{j=1}^{N} hat{gamma}_{jk}}{N} ]
重复以上计算,知道对数似然函数值不再有明显的变化为止。
算法(高斯混合模型参数估计的 EM 算法)
输入: 观测数据 (y_1, y_2, cdots, y_N),高斯混合模型;
输出:高斯混合模型参数。
(1)取参数的初始值开始迭代;
(2)E 步:依据当前模型参数,计算分模型 (k) 对观测数据 (y_j) 的响应度
(3)M 步:计算新一轮迭代的模型参数
(4)重复第(2)步和第(3)步,知道收敛。
3 高斯混合模型的应用
3.1 AIC 和 BIC
待补充
3.2 高斯混合模型用于聚类
# 导入模块
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture
import matplotlib.pyplot as plt
# 生成数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
确定簇的数量:
n_components = np.arange(1, 21)
models = [GaussianMixture(n, covariance_type='full', random_state=0).fit(X) for n in n_components]
# plt.figure(figsize=(8, 6))
plt.plot(n_components, [m.bic(X) for m in models], label='BIC')
plt.plot(n_components, [m.aic(X) for m in models], label='AIC')
plt.legend(loc='best')
plt.xticks(range(0, 22))
plt.xlabel('n_components')
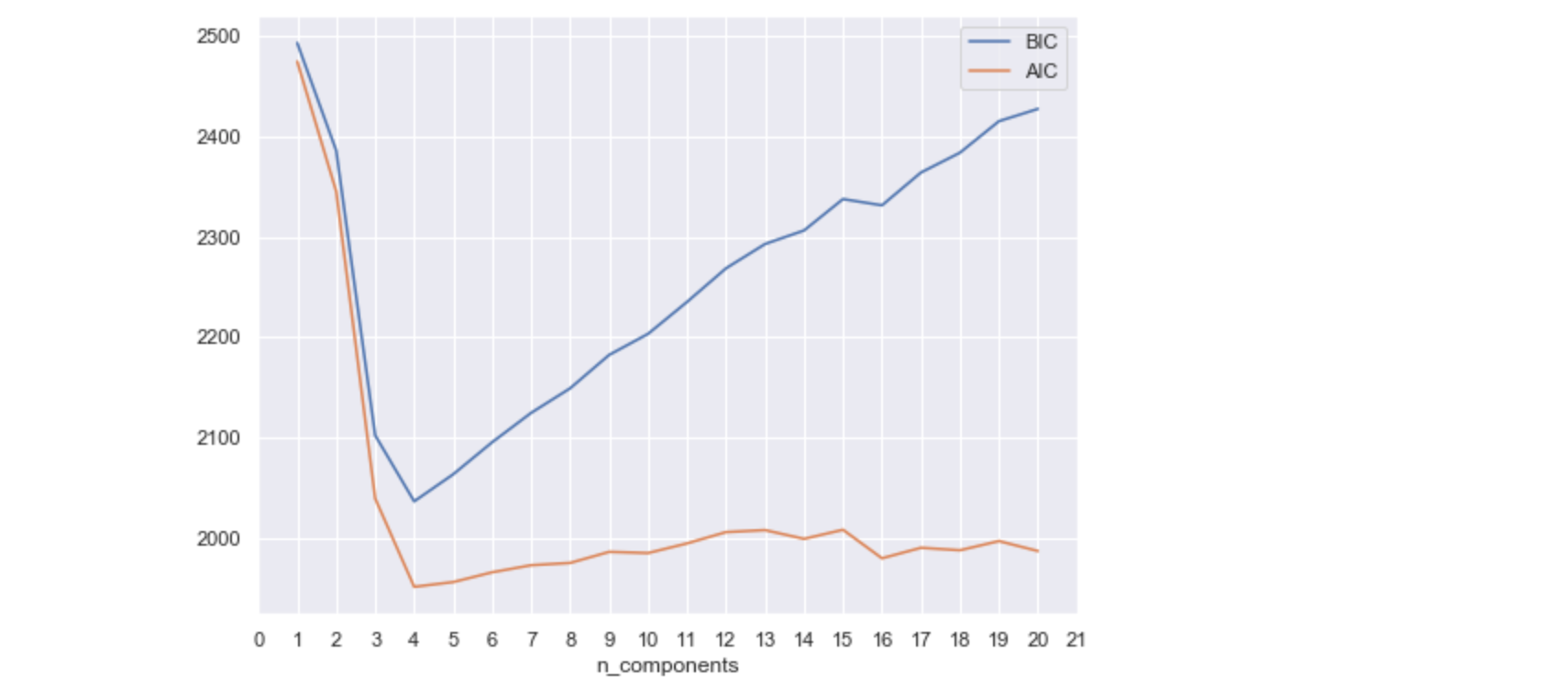
我们使用最佳聚类数(在这种情况下为4)训练模型,并将聚类结果和原始数据进行对比:
gmm = GaussianMixture(n_components=4, init_params='kmeans') # 参数初始化方法
gmm.fit(X)
y_pred = gmm.predict(X)
figure, axes = plt.subplots(1, 2, figsize=(10, 4), dpi=100)
axes[0].scatter(X[:,0], X[:,1], c=y, cmap='rainbow')
axes[0].set_title("original clusters")
axes[1].scatter(X[:,0], X[:,1], c=y_pred, cmap='rainbow')
axes[1].set_title("GMM clusters")
plt.show()

3.3 高斯混合模型和 K-Means 的异同
高斯混合模型与 K-Means 算法的相同点是:
(1)它们都是可用于聚类的算法;
(2)都需要指定 K 值;
(3)都是使用 EM 算法来求解;
(4)都往往只能收敛于局部最优。
而它相比于 K 均值算法的优点是:
(1)可以给出一个样本属于某类的概率是多少;
(2)不仅仅可以用于聚类,还可以用于概率密度的估计;
(3)并且可以用于生成新的样本点。
参考
- 《统计学习方法》 李航
- 高斯混合模型(Gaussian Mixture Model)与EM算法原理
- 如何通俗的理解高斯混合模型(Gaussian Mixture Models)
- 《百面机器学习》