B 树形dp
组合的思想。
Z队长的思路。
dp[i][1]表示以i为跟结点的子树向上贡献1个的方案,dp[i][0]表示以i为跟结点的子树向上贡献0个的方案.
如果当前为叶子节点,dp[i][0] = 1,(颜色为1,可以断开与父节点的连接,颜色为0,不断开,方案恒为1),dp[i][1] = co[i](i节点的颜色)。
非叶子节点:将所有孩子节点的dp[child][0]乘起来为sum,孩子贡献为0的总方案。
当前颜色为0时, dp[i][1] += sum/dp[child][0]*dp[child][1],(选当前孩子贡献的1) ,
dp[i][0] = sum+dp[i][1](将i与其父亲断开)。
当颜色为1时, dp[i][1] (需儿子们贡献为0)= dp[i][0](需与父亲断开) = sum.
中间除法取模需要用到逆元。 (s/y)%mod = (s*y^mod-2)%mod;

1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<stdlib.h> 6 #include<vector> 7 #include<cmath> 8 #include<queue> 9 #include<set> 10 using namespace std; 11 #define N 100010 12 #define LL long long 13 #define INF 0xfffffff 14 #define mod 1000000007 15 const double eps = 1e-8; 16 const double pi = acos(-1.0); 17 const double inf = ~0u>>2; 18 vector<int>ch[N]; 19 int dp[N][2]; 20 int co[N]; 21 LL q_mod(LL a,LL b) 22 { 23 LL d,t; 24 d = 1,t=a; 25 while(b) 26 { 27 if(b&1) d = (d*t)%mod; 28 b/=2; 29 t = (t*t)%mod; 30 } 31 return d; 32 } 33 LL cal(LL s,LL y,LL x) 34 { 35 s = (s*x)%mod; 36 return (s*q_mod(y,mod-2))%mod; 37 } 38 void dfs(int u,int pre) 39 { 40 int i; 41 LL s0=1; 42 int flag = 0; 43 for(i = 0 ; i < ch[u].size() ;i++) 44 { 45 int v = ch[u][i]; 46 if(v==pre) continue; 47 flag = 1; 48 dfs(v,u); 49 s0 = (s0*dp[v][0])%mod; 50 } 51 if(!flag) 52 { 53 dp[u][0] = 1; 54 dp[u][1] = co[u]; 55 return ; 56 } 57 if(co[u]==0) 58 { 59 dp[u][0] = s0; 60 dp[u][1] = 0; 61 for(i = 0 ;i < ch[u].size() ; i++) 62 { 63 int v = ch[u][i]; 64 if(v==pre) continue; 65 if(!dp[v][1]) continue; 66 dp[u][1] = (dp[u][1]+cal(s0,dp[v][0],dp[v][1]))%mod; 67 } 68 dp[u][0] = (dp[u][0]+dp[u][1])%mod; 69 } 70 else 71 { 72 dp[u][0] = s0; 73 dp[u][1] = s0; 74 } 75 } 76 int main() 77 { 78 int n,i; 79 cin>>n; 80 for(i = 0 ; i < n-1; i++) 81 { 82 int u; 83 scanf("%d",&u); 84 ch[u].push_back(i+1); 85 ch[i+1].push_back(u); 86 } 87 for(i = 0 ; i < n; i++) 88 scanf("%d",&co[i]); 89 dfs(0,-1); 90 cout<<dp[0][1]<<endl; 91 return 0; 92 }
C 标记数组开始和尾部 线段树维护。
因为有翻转操作,当前数组的开始与结尾不确定,用两个变量标记。
线段树节点表示以它为右端点的线段 比如 0-1-2-3-4-5-6 分别用1 2 3 4 5 6表示它左边那条线段。
如果旋转位置大于当前线段长度的一半,先把此线段翻转,再翻转相对的较短一段。
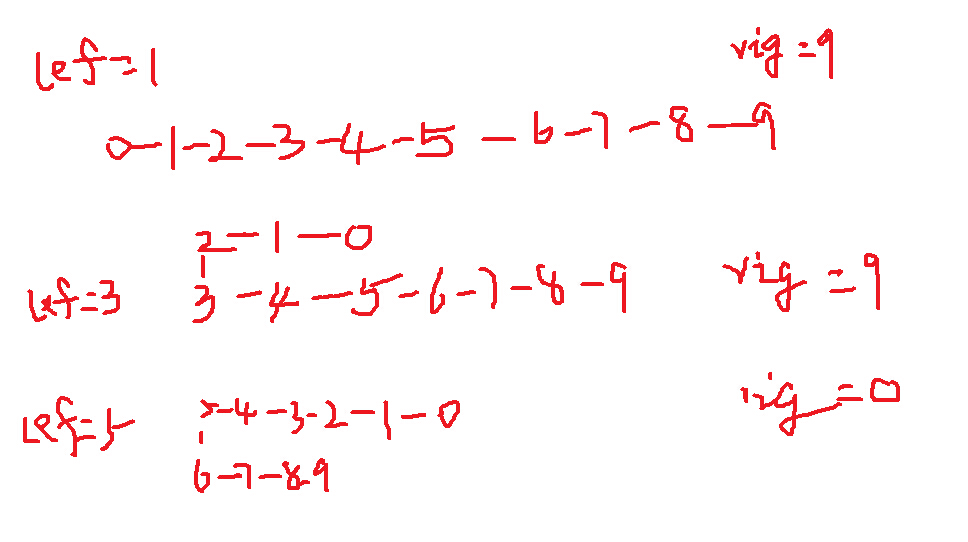

1 #include <iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<stdlib.h> 6 #include<vector> 7 #include<cmath> 8 #include<queue> 9 #include<set> 10 using namespace std; 11 #define N 100000 12 #define LL long long 13 #define INF 0xfffffff 14 const double eps = 1e-8; 15 const double pi = acos(-1.0); 16 const double inf = ~0u>>2; 17 int s[N<<2]; 18 int a[N]; 19 void up(int w) 20 { 21 s[w] = s[w<<1]+s[w<<1|1]; 22 } 23 void build(int l,int r,int w) 24 { 25 if(l==r) 26 { 27 s[w] = a[l] = 1; 28 return ; 29 } 30 int m = (l+r)>>1; 31 build(l,m,w<<1); 32 build(m+1,r,w<<1|1); 33 up(w); 34 } 35 void update(int p,int d,int l,int r,int w) 36 { 37 if(l==r) 38 { 39 s[w]+=d; 40 a[l] = s[w]; 41 return ; 42 } 43 int m = (l+r)>>1; 44 if(p<=m) update(p,d,l,m,w<<1); 45 else update(p,d,m+1,r,w<<1|1); 46 up(w); 47 } 48 int query(int a,int b,int l,int r,int w) 49 { 50 if(a<=l&&b>=r) 51 { 52 return s[w]; 53 } 54 int m = (l+r)>>1; 55 int res = 0; 56 if(a<=m) res+=query(a,b,l,m,w<<1); 57 if(b>m) res+=query(a,b,m+1,r,w<<1|1); 58 return res; 59 } 60 int main() 61 { 62 int n,m,i,j; 63 cin>>n>>m; 64 build(1,n,1); 65 int lef=1,rig=n; 66 while(m--) 67 { 68 int x,y,z; 69 scanf("%d%d",&x,&y); 70 if(x==1) 71 { 72 int mid = (abs(rig-lef)+1)>>1; 73 //cout<<mid<<" .."<<rig<<" "<<lef<<endl; 74 if(y>mid) 75 { 76 swap(lef,rig); 77 y = abs(rig-lef)+1-y; 78 } 79 //cout<<y<<".."<<endl; 80 int st,en; 81 if(lef<rig) 82 { 83 st = lef+y-1; 84 j = st+1; 85 for(i = st ; i >= lef ; i--) 86 { 87 update(j,a[i],1,n,1); 88 j++; 89 } 90 lef = st+1; 91 } 92 else 93 { 94 st = lef-y+1; 95 j = st-1; 96 for(i = st ;i <= lef ;i++) 97 { 98 update(j,a[i],1,n,1); 99 j--; 100 } 101 lef = st-1; 102 } 103 } 104 else 105 { 106 scanf("%d",&z); 107 y++; 108 int ll,rr; 109 if(lef>rig) 110 { 111 ll = lef-z+1; 112 rr = lef-y+1; 113 } 114 else 115 { 116 ll = lef+y-1; 117 rr = lef+z-1; 118 } 119 cout<<query(ll,rr,1,n,1)<<endl; 120 } 121 } 122 return 0; 123 }
