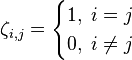中国剩余定理

维基百科，自由的百科全书

中国剩余定理（Chinese Remainder Theorem，中国余数定理），古有“韩信点兵”、“孙子定理”、“鬼谷算”、“隔墙算”、“剪管术”、“秦王暗点兵”、“物不知数”之名，是数论中的一个重要命题。

[编辑] 物不知数

在中国古代著名数学著作《孙子算经》中，有一道题目叫做“物不知数”，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。

中国数学家秦九韶于1247年做出了完整的解答，口诀如下

三人同行七十希，五树梅花廿一支，七子团圆正半月，除百零五便得知

这个解法实际上是，首先利用秦九韶发明的大衍求一术求出5和7的最小公倍数35的倍数中除以3余数为1的最小一个70（这个称为35相对于3的数论倒数），3和7的最小公倍数21相对于5的数论倒数21，3和5的最小公倍数15相对于7的数论倒数15。然后

$70 \times 2 + 21 \times 3 + 15 \times 2 = 233$

233便是可能的解之一。它加减3、5、7的最小公倍数105的若干倍仍然是解，因此最小的解为233除以105的余数23。

附注：这个解法并非最简，因为实际上35就符合除3余2的特性，所以最小解是： $35 \times 1 + 21 \times 3 + 15 \times 2- 3 \times 5 \times 7 = 128 - 105 = 23$ 最小解加上105的正整数倍都是解。

[编辑] 形式描述

以上解法若推广到一般情况，便得到了中国剩余定理的一个构造性证明。

一般地，中国剩余定理是指若有一些两两互质的整数 $m_1, m_2, \ldots, m_n$ ，则对任意的整数： $a 1, a 2,... a n$ ，以下联立同余方程组对模 $m_1 m_2 \cdots m_n$ 有公解：

$\left\{ \begin{matrix} x \equiv a_1 \pmod {m_1} \\ x \equiv a_2 \pmod {m_2} \\ \vdots \qquad\qquad\qquad \\ x \equiv a_n \pmod {m_n} \end{matrix} \right.$

[编辑] 克罗内克符号

为了便于表述，对任意的正整数 $\mathbf{i,j}$ 用一个常用函数 $ζ i, j$ 表示，称之为克罗内克符号(Kronecker).定义：

$\zeta_{i,j} =\begin{cases} 1, \; i=j \\ 0, \; i \ne j \end{cases}$

使用该符号，即可给出上述一般同余方程组的求解过程，分两步完成

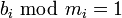对每个 $1 \le i \le k$ ，先求出正整数 $b i$ 满足 $b_i \equiv \zeta_{i,j} \pmod {m_j}$ ，即所求的 $b i$ 满足条件： $b_i \;\bmod\; m_i = 1$ ，但被每个 $m_j(i\ne j)$ 整除。其求法如下：记 $r_i =m_{1} \cdots m_{i-1} m_{i+1} \cdots m_k$ ，根据条件 $m_1 ,\cdots,m_k$ 两两互素，可知 $r i$ 和 $m i$ 也互素，故存在整数 $c i$ 和 $d i$ 使得 $r i c i + m i d i = 1$ .令 $b i = r i c i$ ，则对每个 $i \ne j$ ，相对应的 $m j$ 显然整除 $b i$ ，并且 $b_i \equiv 1 \pmod {m_i}$ 。由此表明 $b i$ 即为所求。
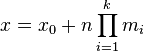对于前述所求的 $b i$ ，令 $x_0 = \sum_{i=1}^k a_ib_i$ ，则 $x_0 \equiv a_i b_i \equiv a_i \pmod {m_i}$ ，这说明 $x 0$ 为上述同余方程组的一个解，从而所有的解可表示为 $x = x_0 + n \prod_{i=1}^k m_i$ ，其中的n可以取遍所有的整数。

[编辑] 近世交换环及推广

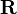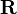设 $\mathbf{R}$ 为有单位元的交换环， $I_1,\cdots,I_n$ 为环 $\mathbf{R}$ 的理想，并且当 $i \ne j$ 时， $I_i + I_j = \mathbf{R}$ ，则有典范的环同构 $\mathbf{R} /( I_1 \cap \cdots \cap I_n \cong \mathbf{R} / I_1 \times \cdots \times \mathbf{R} I_n$ ，其中环同构由映射 $\alpha + I_1 \cap \cdots \cap I_n \rightarrow (\alpha + I_1 , \alpha + I_2 ,\cdots, \alpha + I_n$ ）给出。

模板

 1 ll x,y;
 2  ll ext_eulid(ll a,ll b)
 3  {
 4      int t,d;
 5      if(b == 0)
 6      {
 7          x = 1;
 8          y = 0;
 9          return a;
10      }
11      d = ext_eulid(b,a%b);
12      t = x;
13      x = y;
14      y = t - (a/b)*y;
15      return d;
16  }
17  ll CRT(ll *p,ll *o,int num)//p数组代表余数，o数组代表互质的数
18  {
19      int i;
20      ll ans = 0,n = 1;
21      for(i = 1;i <= num;i ++)
22      {
23          n *= o[i];
24      }
25      for(i = 1;i <= num;i ++)
26      {
27          ext_eulid(n/o[i],o[i]);
28          x = (x+o[i])%o[i];
29          ans = (ans + n/o[i]*p[i]*x) % n;
30      }
31      return ans;
32  }

http://poj.org/problem?id=1006

未用模板解法求解基础数

View Code

 1 #include <iostream>
 2 #include<cstdio>
 3 #include<string.h>
 4 using namespace std;
 5 int base(int x,int a,int p)
 6 {
 7     int i;
 8     int y = a;
 9     if((a%x!=0&&p%x==0)||(a%x==0&&p%x!=0))
10     return 0;
11     if(a%x!=p%x)
12     {
13         for(i = 1; ;i++)
14         {
15             a = y*i;
16             if(a%x==p%x)
17             break;
18         }
19     }
20     return a;
21 }
22 int main()
23 {
24     int p,e,i,d,j,k = 0;
25     int y = 21252;
26     int a = y/23;
27     int b = y/28;
28     int c = y/33;
29     while(cin>>p>>e>>i>>d)
30     {
31         k++;
32         if(p==-1&&e==-1&&i==-1&&d==-1)
33         break;
34         int a1 = base(23,a,p);
35         int b1 = base(28,b,e);
36         int c1 = base(33,c,i);
37         int s = a1+b1+c1;
38         printf("Case %d: ",k);
39         if(s%y==0)
40         s=y;
41         else
42         {
43             s = s%y;
44             if(s<=d)
45             s+=y;
46         }
47         printf("the next triple peak occurs in %d days.\n",s-d);
48     }
49     return 0;
50 }

套模板