旅行商问题
BTBU-JY143班共有30位同学,来自22个地区,我们希望在假期来一次说走就走的旅行,将所有同学的家乡走一遍。算起来,路费是一笔很大的花销,所以希望设计一个旅行方案,确保这一趟走下来的总路程最短。
旅行商问题是一个经典的NP问题
NP就是Non-deterministic Polynomial,即多项式复杂程度的非确定性问题,是世界七大数学难题之一。
如果使用枚举法求解,22个地点共有:
(22-1)!/2 = **25545471085854720000 **种路线方案
GA算法
遗传算法将“优胜劣汰,适者生存”的生物进化原理引入优化参数形成的编码串联群体中,按所选择的适应度函数并通过遗传中的复制、交叉及变异对个体进行筛选,使适应度高的个体被保留下来,组成新的群体,新的群体既继承了上一代的信息,又优于上一代。这样周而复始,群体中个体适应度不断提高,直到满足一定的条件。遗传算法的算法简单,可并行处理,并能到全局最优解。
GA算法设计
1.生成原始染色体种群
采用实数编码,以N个城市的序号作为一条可能的路径。 例如对8个城市,可生成如下的染色体代表一条路径,8,6,4,2,7,5,3,1.重复操作生成数目等于n的染色体种群。
2.生成适应度函数
由于是求最短路径,适应度函数一般求函数最大值,所以取路径总长度T的倒数,即fitness=1/T。
3.选择染色体
采用轮盘赌的方式产生父代染色体。
4.对染色体种群进行编码
假设有一个含有九个城市的列表:W=(A,B,C,D,E,F,G,H,I)。
有如下两条路线:
W1=(A,D,B,H,F,I,G,E,C)
W2=(B,C,A,D,E,H,I,F,G)
则这两条路线可编码为:
W1=(142869753)
W2=(231458967)
5.交叉
以概率Pc选择参加交叉的个体(偶数个),用两点交叉算子进行操作。
例如对于下面两个染色体个体
(1 3 4 | 5 2 9 | 8 6 7)
(1 7 6 | 9 5 2 | 4 3 8)
通过两点交叉可得到子代染色体为
(1 3 4 | 9 5 2 | 8 6 7)
(1 7 6 | 5 2 9 | 4 3 8)
6.变异
以概率Pm选择参加变异的个体,用对换变异进行操作。随机的选择个体中的两个位点,进行交换基因。
如A=123456789;如果对换点为4和7,则经过对换后为B=123756489
7.解码
对染色体进行解码,恢复染色体的实数表示方法。
8.逐代进化
根据得出的新的染色体,再次返回选择染色体的步骤,进行迭代,直到达到迭代次数,算法停止。
算法实现##
#加载packages
library(sp)
library(maptools)
library(geosphere)
source("C:\Users\ShangFR\Desktop\路径优化\GA算法脚本.R")
data=read.csv("C:\Users\ShangFR\Desktop\路径优化\143地理坐标.csv") #读取城市经纬度数据
border <- readShapePoly("C:\Users\ShangFR\Desktop\路径优化\map\bou2_4p.shp") #读取各省的边界数据等
#初始化(列出地区距离矩阵-聚类)
da=data[,1:2]
rownames(da)=data[,3]
hc=hclust(dist(da))
cutree(hc, h = 10)
plot(hc)
route=CreatDNA(data,5)
x = route[,1]
y = route[,2]
z = route[,3]
cols=route[,4]
muer.lonlat = cbind(route[,1],route[,2]) # matrix
muer.dists = distm(muer.lonlat, fun=distVincentyEllipsoid) # 精确计算,椭圆
ans=round(muer.dists/1000,2)
roundots = list(x=x,y=y,ans=ans,z=z,cols=cols)
species = GA4TSP(dots=roundots,initDNA=NULL,N=50,cp=0.1,vp=0.01,maxIter=1000,maxStay=100,maxElite=2,drawing=TRUE)
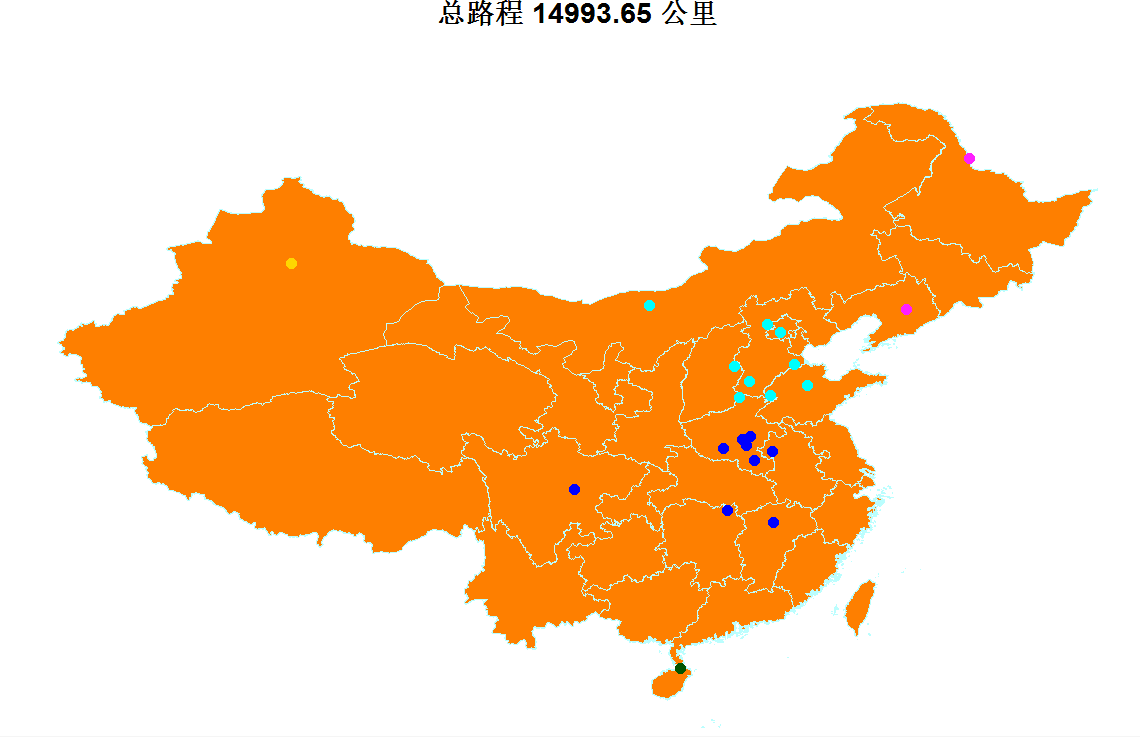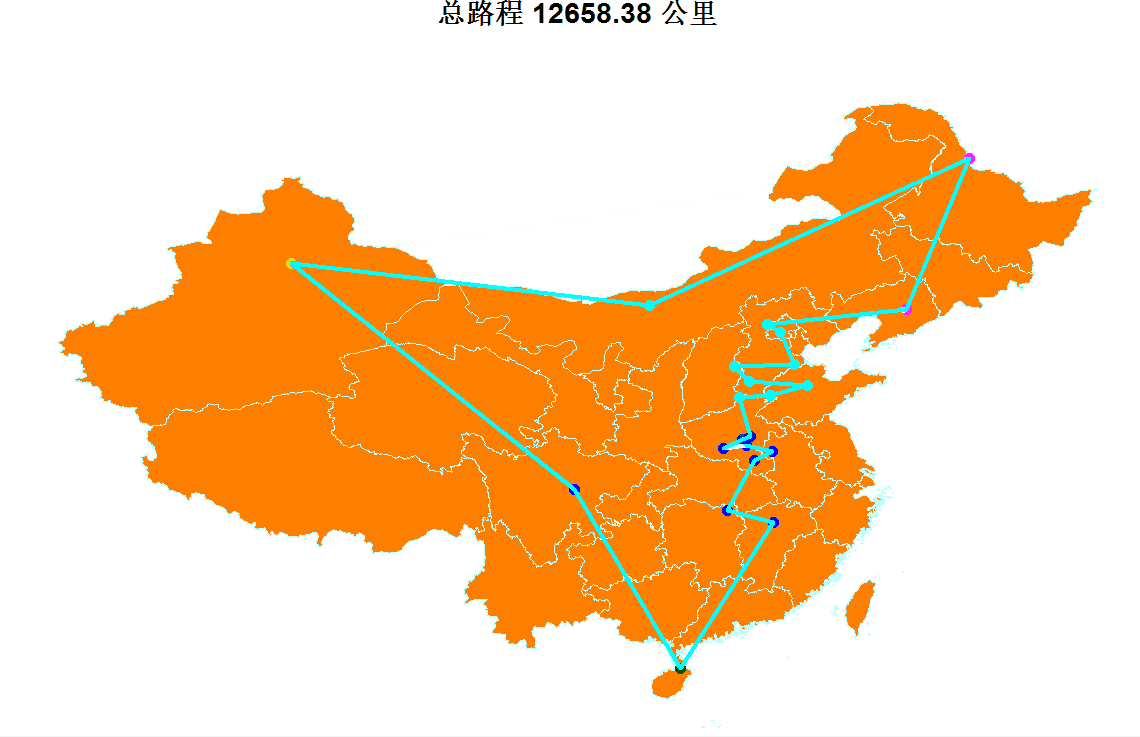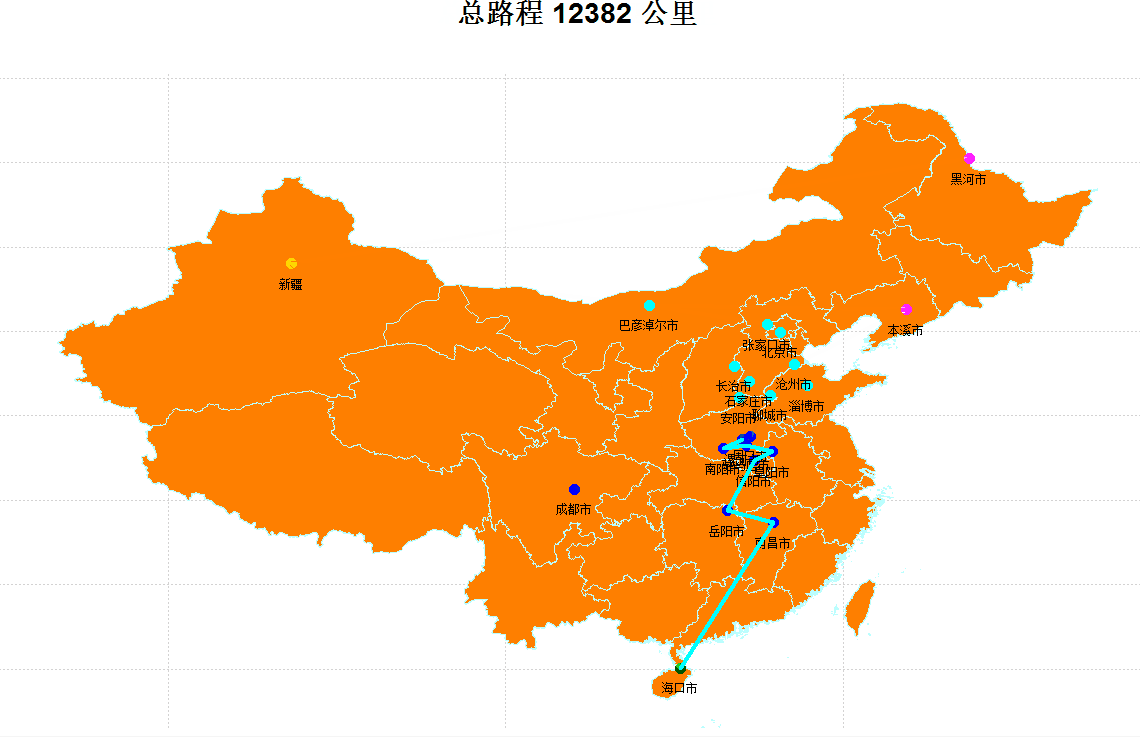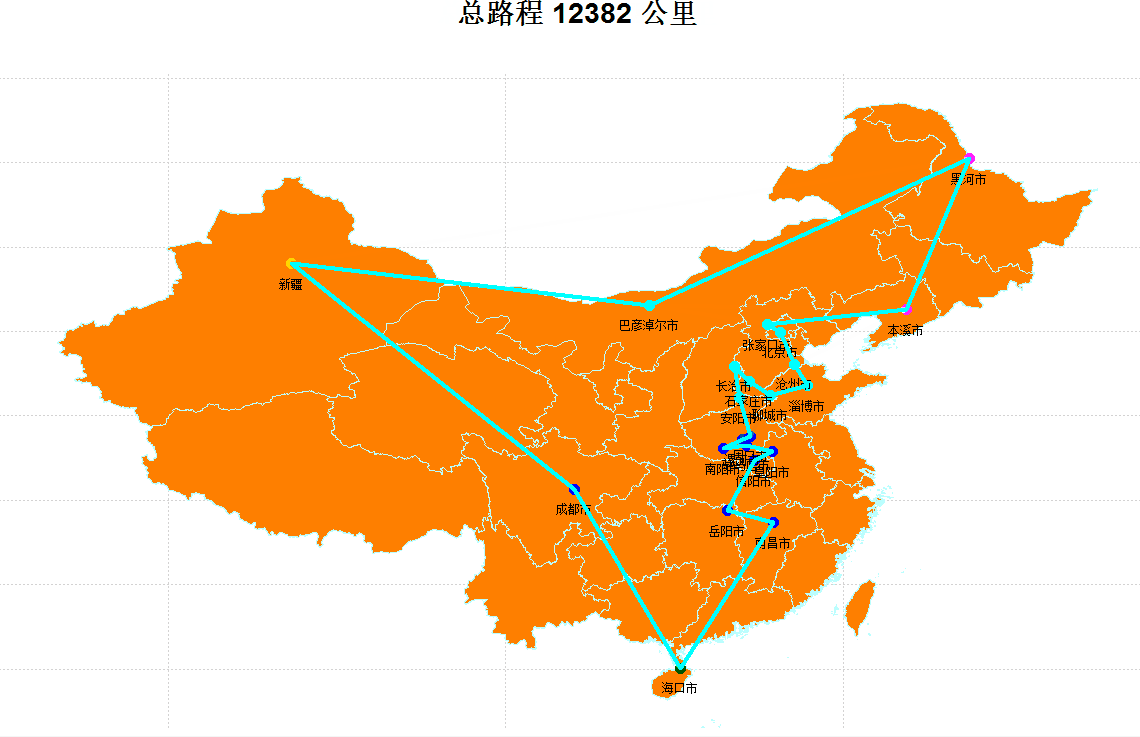
最优路径可视化
[此图基于百度Echarts](http://echarts.baidu.com/)详细介绍
反馈与建议
- 作者:ShangFR
- 邮箱:shangfr@foxmail.com
感谢您阅读这份文档,分享。