极大似然估计是一种用已知的样本数据分布去推测具体的分布情况统计学的方法。
使用极大似然估计方法的两个条件:1.假定数据服从某种已知的特定数据分布型;2.已经得到了一定的数据集。
以下用估计馒头重量的分布情况举例。
背景:对食堂所卖馒头的重量进行估计。根据现统计知识,可以假定某一日食堂所做的全部馒头的重量分布是符合正态分布的。随机抽取其中的100个称重。
那么如何用这 100 馒头重量的数据集 D 去推测这一天所有馒头的重量分布呢?
可将这 100 馒头重量的数据集 D 记作: 。D服从一个数学期望为μ、标准方差为σ2的正态分布(也叫高斯分布),记为: D∼N(μ,σ2)。
。D服从一个数学期望为μ、标准方差为σ2的正态分布(也叫高斯分布),记为: D∼N(μ,σ2)。
 极大似然估计并不是百分百准确,但在数据量足够的情况下,还是可信的。目标就是关于L(θ)函数最大值时参数向量θ的取值,但在实际情况下我们会取对数
极大似然估计并不是百分百准确,但在数据量足够的情况下,还是可信的。目标就是关于L(θ)函数最大值时参数向量θ的取值,但在实际情况下我们会取对数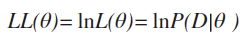
参考文章:https://www.jianshu.com/p/e0eb4f4ccf3e
 。D服从一个数学期望为μ、标准方差为σ2的正态分布(也叫高斯分布),记为: D∼N(μ,σ2)。
。D服从一个数学期望为μ、标准方差为σ2的正态分布(也叫高斯分布),记为: D∼N(μ,σ2)。其中,期望
μ 决定了分布图形在坐标轴中的位置,标准差 σ 决定了分布图形的幅度。此时要解决的问题就是如何确定参数 μ 和
σ。为了方便行事,一般把参数写成一个参数向量 θ =(μ,σ)。把在参数向量 θ 下的正态分布下,某一重量的馒头是标准馒头的概率密度写做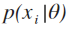 。我们将统计到的 100 个馒头重量的数据集 D 在参数向量 θ 下的正态分布下可能性用连乘处理
。我们将统计到的 100 个馒头重量的数据集 D 在参数向量 θ 下的正态分布下可能性用连乘处理

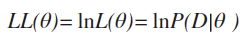
取对数可以把连乘转化成累加,更加方便于求偏导计算极值。根据分布函数不同,具体求解似然函数的过程也有所差异。
参考文章:https://www.jianshu.com/p/e0eb4f4ccf3e