批量建堆（二叉堆【完全二叉堆】）~~批量建堆

 批量建堆

1，逻辑：局部建立堆---》整体建立堆

2，其实就是一个调整范围的确定 + 考虑当前结点的身份（作为子结点或父结点）而已。

■ 上滤（自上而下的上滤【本质就是添加】）—----当前结点作为子节点，考虑它作为子结点在当前位置是否合适。

■ 下滤（自下而上的下滤【本质就是删除】）------当前结点作为父结点，考虑它作为父结点在当前位置是否合适。

❀ 上滤建立堆-----逻辑就是添加时的上滤操作-是添加到数组的最后一个位置，然后不断地往上比（比较的终点是根），当前结点与它的父结点比较【直到找到合适位置】

❀ 下滤建立堆----逻辑就是符合删除操作~从第一个非叶子结点开始（比较的终点是根），当前结点不断地与它的最大子结点比较【直到找到合适位置】

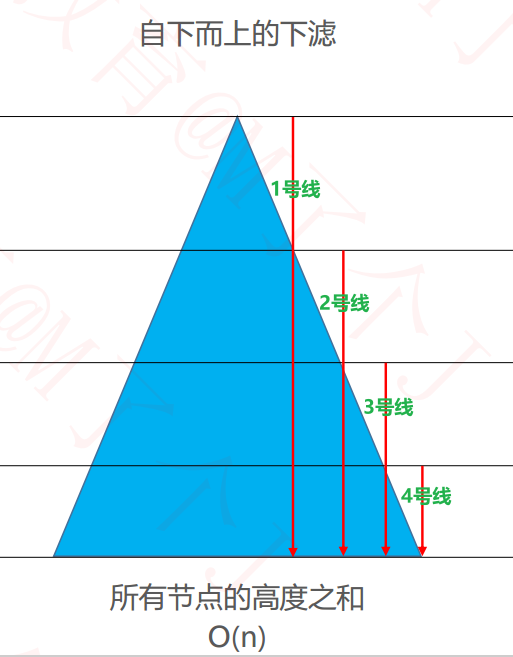
■ 最大堆----批量建堆-效率对比：上滤与下滤比较----同线比较

例如：拿1号线作比较，可以看到上滤与下滤比较：

上滤可能移动的结点比较多（往上跑的结点数量比较多），

下滤可能移动的结点比较少（往下跑的结点数量比较少）

   

● 添加代码（咱使用的数据结构是数组）：

    @Override
    public void add(E element) {
        //检查元素是否具有可比较性【排除null】
        elementNotFoundCheck(element);
        // 扩容检查、扩容操作
        ensureCapacity(size + 1);
        //按数组添加特点【每次都是添加到最后的位置,添加完数组长度++】
        elements[size++] = element;
        //维持二叉堆的特点【大根堆特点】~ 上滤
        siftUp(size -1);
        
    }

 ● 上溢代码：

    /**
     * 上滤【从最后一个位置开始往上 】
     * 【插入到原逻辑的优化，插入到最后一个位置时，比较当前结点的父结点是否还是大于
　　  * 【插入结点，若是满足，即找到合适位置，否则，当前结点的父结点要变成子结点啦，然后爬升到父结点的位置继续比较】】
     */
    private void siftUp(int index) {        
        // 插入element 随着比较不断的上移【选择一个合适的位置（插入的当前结点比父结点小）】，而是最终确定位置后，放一下]
        E element = elements[index]; 
        while (index > 0) {
            int parentIndex = (index - 1) >> 1;
            E parent = elements[parentIndex];
            if (compare(element, parent) <= 0) break;
            //让比较小的父元素放到子元素位置
            elements[index] = parent;
            
            // 重新赋值index
            index = parentIndex;
        }
        elements[index] = element;//找到最终的位置index
    }

● 删除代码：

    @Override
    public E remove() {
        emptyCheck();//检查数组是否为空
        E root = elements[0];
        int lastIndex = --size;
        elements[0] =  elements[lastIndex];
        elements[lastIndex] = null;
            
        //下滤
        siftDown(0);    //根据索引进行下滤操作
    
        return root;
    }

● 下溢代码：

/**
     * 下滤：删除操作【从第 index 位置开始，往下】
     * 即从当前结点开始往下比（跟最大孩子结点比），直到找到合适的位置【满足 当前结点的值（作为父结点）大于子结点的值】
     * 当出现了最大子结点大于父结点时，子结点的值覆盖到父节点的位置
     * @param index
     */
    private void siftDown(int index) {
        /**
         * 非叶子结点个数： n1 + n2 = floor(n /2);【最后一个非叶子结点索引即：(size/2) - 1】
         * 叶子结点个数：n0 = floor((n + 1) /2);
         *结论：第一个叶子结点的索引就是非叶子结点的数量【从上到下，从左到右，非叶子-》叶子】
         */
//        while(index < 第一个叶子结点的索引)【即保证index 都是非叶子结点】
        
        int half = size >> 1;
        E element = elements[index];
        while(index < half) {
            //完全二叉树：只能有两种情况：
            //1，只有 左结点
            //2，有左，有右
            //默认假设左结点是最大结点
            int childIndex = (index << 1) + 1;//左结点的索引要注意【位移符号的书写的方向】
            E childElement = elements[childIndex];
            
            //rightIndex < size [说明右结点存在，处于合理区间|，即存在]
            int rightIndex = childIndex + 1;
            if(rightIndex < size
                    && compare(elements[rightIndex], childElement) > 0) {
                childIndex = rightIndex;
                childElement = elements[rightIndex];
                //优化一下代码写法：
//                childElement = elements[childIndex = rightIndex];
            }
            
            
            //用当前结点的最大子结点和当前结点进行比较【当前大的话】
            //bug:if(compare(elements[index], childElement) >= 0)
            //错误：咱是要将element 找到合适位置呀，element 是固定的呀，不是 elements[index]
            if(compare(element, childElement) >= 0) break;
            //子结点大的话
            elements[index] = childElement;
            index = childIndex;
        }
        elements[index] = element;
    }