数据结构~基础2~树【《二叉树、二叉搜索树、AVL树、B树、红黑树》的设计】~二叉树
● 树的形状:【左子树(左区间)】 根(父结点)【右子树(右区间)】
❀ 为啥遍历是不断沿着左子树爬下下一层~~~为了实现拿到当前层的第一个结点。
❀ 对于树的遍历,到下一层,在形式上是先到了“根”(父结点)上。
1、二叉树之通用的接口【遍历】:
● 前序遍历: 根(父) 左子树 右子树 | 根(父) 右子树 左子树 【前序只需满足 根最先访问】
● 中序遍历:左子树 根(父) 右子树 | 右子树 根(父) 左子树 【中序只需满足 根中间访问】
● 后序遍历: 左子树 右子树 根(父) | 右子树 左子树 根(父) 【后序只需满足 根最后访问】
● 层序遍历: 一层一层的结点从左到右进行访问。
❀ 二叉树的通用接口:遍历[前序、中序、后序、层序、允许外界遍历二叉树的元素(设计接口)+增强遍历] + 前驱、后驱结点
+ 树的深度 + 是否为完全二叉树
1,前序遍历:
■ 递归:根 左 右
■ 迭代:【使用栈】:不断地下一层【通过node.left方式】:不断地拿到下一层的根,将根数据进行添加,
直到到达最后一层【node.left = null】,pop出当前的根结点,通过其切换到右子树。
□ 前序遍历的代码:
//递归实现
// 前序遍历需要传入一个结点(根结点),然后才能开始遍历 private void preorderTraversal(Node<E> node) { // 不断地遍历,终有一空便结束 if (node == null) return; System.out.println(node.elmement); preorderTraversal(node.left); preorderTraversal(node.right); }
//迭代实现【并将结果存储到List】
public List<Integer> preorderTraversal1(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if (root == null) { return res; } //遍历过的点,不要了可以pop()掉,不断的pop(),然后才能拿到当前结点的右结点(先是不断的更新结点为左结点) //然后没有左结点了,开始pop() 一层(一个结点) Deque<TreeNode> stack = new LinkedList<TreeNode>(); TreeNode node = root; while (!stack.isEmpty() || node != null) { while (node != null) { res.add(node.val); stack.push(node); node = node.left; } node = stack.pop(); node = node.right; } return res; }
2,中序遍历:
■ 递归:左 根 右
■ 迭代:【使用栈】:不断地下一层【通过node.left方式】:不断地拿到下一层的根,
直到到达最后一层【node.left = null】,pop出当前的根结点,将当前根的数据进行添加,通过其切换到右子树。
□ 中序遍历的代码:
// 递归:
private void inorderTraversal(Node<E> node) { if (node == null) return; inorderTraversal(node.left); System.out.println(node.elmement); inorderTraversal(node.right); }
// 迭代 public List<Integer> inorderTraversal2(TreeNode root) { List<Integer> list2 = new ArrayList<>(); if (root == null) return list2; Deque<TreeNode> stack = new LinkedList<>(); TreeNode node = root; while(node != null || !stack.isEmpty() ) { while(node != null) { stack.push(node); node = node.left; } node = stack.pop(); list2.add(node.val); //已经拿到当前结点了 node = node.right; } return list2; }
3,后序遍历:
■ 递归:左 右 根
■ 迭代:【使用栈】:不断地下一层【通过node.left方式】:不断地拿到下一层的根,
直到到达最后一层【node.left = null】,pop出当前的根结点,考虑右结点:【情况一:右边结点存在,将根push回去,切换到右子树】
【情况二:右边结点不存在或者当前结点的右结点是上一个遍历过的结点,将当前结点(根)的数据进行添加,并记录前一个结点。】
□ 后序遍历的代码:
// 递归:
private void postorderTraversal(Node<E> node) { if (node == null) return; postorderTraversal(node.left); postorderTraversal(node.right); System.out.println(node.elmement); }
// 迭代 public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>(); if(root == null) return list; Deque<TreeNode> stack = new LinkedList<>(); TreeNode prev = null; while(!stack.isEmpty() || root != null) { while(root != null) { stack.push(root); root = root.left; } root = stack.pop();
//考虑右结点 //右结点不存在,或者右结点是前一个遍历过的结点prev if (root.right == null || root.right == prev) { list.add(root.val); prev = root; root = null; //不加:超出内存 } else { //右结点存在 stack.push(root); root = root.right; } } return list; }
4,层序遍历:
■ 迭代:【使用队列】(使用队列理由:一层一层从左边到右边【父节点A 先于 父结点B,则父节点A 的孩子 会先于 父结点B 的孩子】):
首先先根入队,然后开始不断地取出当前结点,判断当前结点是否有左结点,有入队,是否有右结点,有入队。
// 层序遍历【迭代】 public void levelOrderTraversal() { if (root == null) return; Queue<Node<E>> queue = new LinkedList<>(); queue.offer(root); // 只要队列不为空:就不断的出队,然后入队左右子节点 while (!queue.isEmpty()) { Node<E> node = queue.poll(); System.out.println(node.elmement); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } } }
5,允许外界遍历二叉树的元素(设计接口)+ 增强遍历【这里以层序遍历 和 后序遍历(前序、中序跟后序一样)】
(1)层序遍历:
① 层序遍历【允许外界遍历二叉树的元素的情况的接口设计】

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
② 层序遍历【允许外界遍历二叉树的元素的情况的接口设计】+ 增强遍历:
增强遍历:通过接口方法的返回值,控制遍历的停止(so 接口方法需要写成可以被控制的,例如布尔类型)

----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
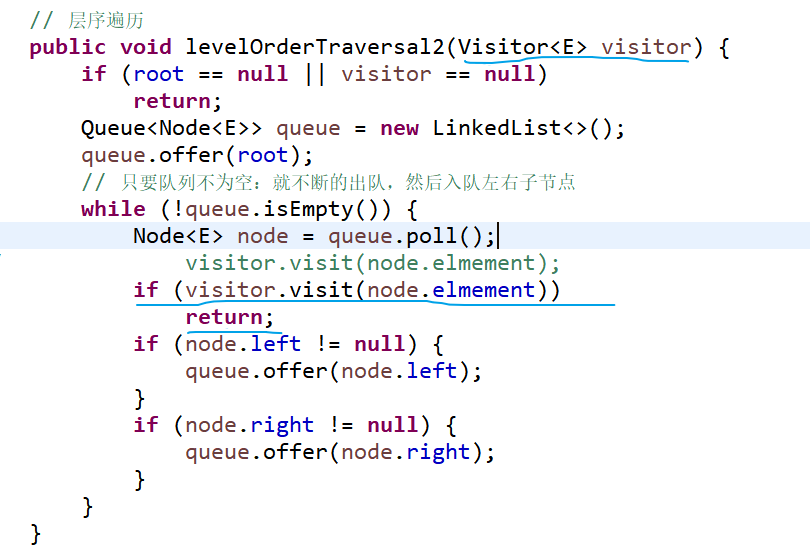
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
(2)后序遍历:
① 后序遍历【允许外界遍历二叉树的元素的情况的接口设计】跟 层序一致(略)
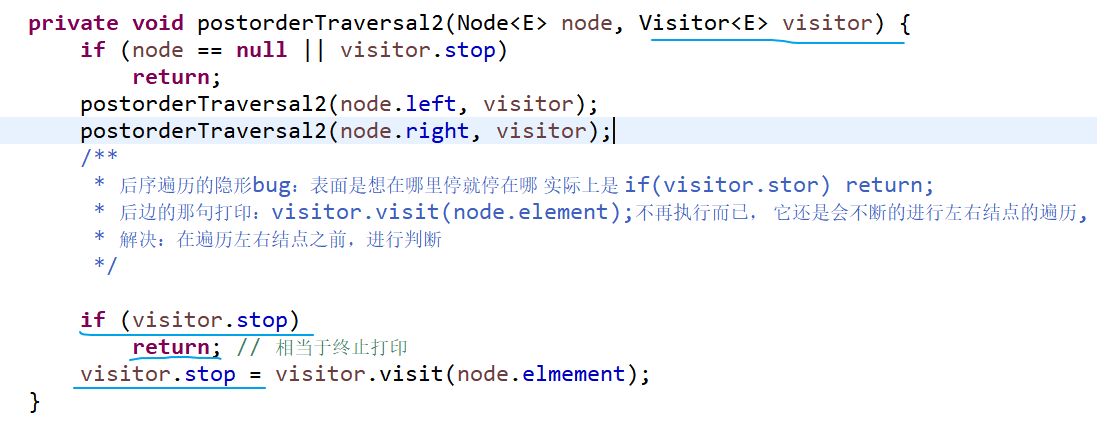
② 后序遍历【允许外界遍历二叉树的元素的情况的接口设计】+ 增强遍历:

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
6,前驱、后驱结点:
■ 前提是:中序遍历才有所谓的前驱和后驱结点。
(1) 前驱结点:中序遍历时的前一个结点。
即:前驱结点(就是比当前结点小的前一个结点)。
● 哪个位置的结点有机会有前驱(根 和 右):
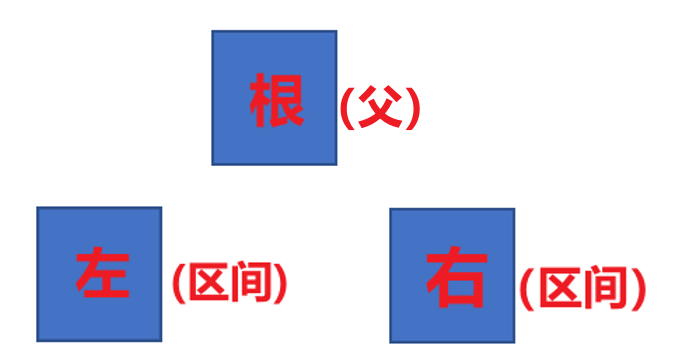
● “前一个结点”:需要离得最近。
①根(看左,找左区间最大的,离得近)
②右(看根,找根)
●方法(接口):
public Node<E> predecessor(Node<E> node){
//当前传入结点(可,需要判断一下:是否有左(有左即可,不需要有右))
node = node.left;
//① 若node 非空:则作为“根”,去左区间找最大的
//② 若node 空:找根(“父结点”),通过判断是否构成“根-右”的关系。【找的过程是逆思维:因为需要遍历 while(“根-左”), 跳出循环则是找到了“根-右”的关系】
}
● 具体代码:
// 前驱结点 public Node<E> predecessor(Node<E> node) { // 有左节点(left.right.right.right...) Node<E> p = node.left; if (p != null) { while (p.right != null) { p = p.right; } return p; } // 没有左节点(视图找到第一个父结点的右结点等于当前结点) // 若一直是父节点左,就继续上一层的父节点 while (node.parent != null && node.parent.left == node) { node = node.parent; } // 来到这里:要么父节点是null,要么是 当前结点是父节点的右结点 return node.parent; }
(2) 后驱结点:分析同理
7,树的深度:
■ 层序遍历+一个辅助变量(用来判断当前层的结点已经遍历到最后一个结点了)实现
8,是否是一棵完全二叉树:
一棵完全二叉树的结点情况分析:
(1)遍历当前结点:有左结点,有右边结点 --正确
(2)有左结点,没有右结点 --正常
(3)没有左结点,有右结点 --不正常
(4)没有左结点,也没有右结点 -- 正常
分析:一旦出现第一个结点没有右结点,则接下来的结点都是叶子结点!【且该过程,一旦出现,有右结点没有左结点的“越界”行为,就false】
■ 完全二叉树的代码:
// 判断是否为完全二叉树(方法二:是构建在只要是二叉树就进行层序遍历基础上,加上特殊情况的判断) public boolean isComplete2() { if (root == null) return false; Queue<Node<E>> queue = new LinkedList<>();// 犯了个错:Queue 是接口,不可直接new // 叶子状态 boolean leaf = false; queue.offer(root); while (!queue.isEmpty()) { // 出队,后入队左右子树结点 Node<E> node = queue.poll(); if (leaf && node.isLeaf()) { return false; } if (node.left != null) { queue.offer(node.left); } else if (node.right != null) { // 否则左边为空,右边不为空 return false; } if (node.right != null) { queue.offer(node.right); } else { // 否则右边为空,左边可能为空,可能不为空【找到第一个空的右结点,接下来的结点都是叶子结点】 // 则开始叶子结点的状态 leaf = true; } } return true; }