04-机器学习_（kmeans聚类算法与应用）

机器学习算法day02_Kmeans聚类算法及应用

课程大纲

Kmeans聚类算法原理	Kmeans聚类算法概述
	Kmeans聚类算法图示
	Kmeans聚类算法要点
Kmeans聚类算法案例	需求
	用Numpy手动实现
	用Scikili机器学习算法库实现
Kmeans聚类算法补充	算法缺点
	改良思路

 

 

 

 

课程目标：

1、理解Kmeans聚类算法的核心思想

2、理解Kmeans聚类算法的代码实现

3、掌握Kmeans聚类算法的应用步骤：数据处理、建模、运算和结果判定

4、

1. Kmeans聚类算法原理

1.1 概述

K-means算法是集简单和经典于一身的基于距离的聚类算法

采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。

该算法认为类簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

 

1.2 算法图示

假设我们的n个样本点分布在图中所示的二维空间。

从数据点的大致形状可以看出它们大致聚为三个cluster，其中两个紧凑一些，剩下那个松散一些，如图所示：

 

 

我们的目的是为这些数据分组，以便能区分出属于不同的簇的数据，给它们标上不同的颜色，如图：

 

 

1.3 算法要点

1.3.1 核心思想

通过迭代寻找k个类簇的一种划分方案，使得用这k个类簇的均值来代表相应各类样本时所得的总体误差最小。

k个聚类具有以下特点：各聚类本身尽可能的紧凑，而各聚类之间尽可能的分开。

 k-means算法的基础是最小误差平方和准则,

其代价函数是：

    

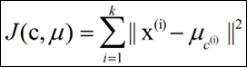
       式中，μc(i)表示第i个聚类的均值。

各类簇内的样本越相似，其与该类均值间的误差平方越小，对所有类所得到的误差平方求和，即可验证分为k类时，各聚类是否是最优的。

上式的代价函数无法用解析的方法最小化，只能有迭代的方法。

 

 

 

 

 

1.3.2 算法步骤图解

下图展示了对n个样本点进行K-means聚类的效果，这里k取2。

 

 

1.3.3 算法实现步骤

k-means算法是将样本聚类成 k个簇（cluster），其中k是用户给定的，其求解过程非常直观简单，具体算法描述如下：

1) 随机选取 k个聚类质心点

2) 重复下面过程直到收敛  {

      对于每一个样例 i，计算其应该属于的类：

          

      对于每一个类 j，重新计算该类的质心：

            

  }

   

其伪代码如下：

********************************************************************

创建k个点作为初始的质心点（随机选择）

当任意一个点的簇分配结果发生改变时

       对数据集中的每一个数据点

              对每一个质心

                     计算质心与数据点的距离

              将数据点分配到距离最近的簇

       对每一个簇，计算簇中所有点的均值，并将均值作为质心

 

 

 

 

  

 

2. Kmeans分类算法Python实战

2.1 需求

对给定的数据集进行聚类

本案例采用二维数据集，共80个样本，有4个类。样例如下：

testSet.txt

1.658985  4.285136

-3.453687 3.424321

4.838138     -1.151539

-5.379713 -3.362104

0.972564     2.924086

-3.567919 1.531611

0.450614   -3.302219

-3.487105 -1.724432

2.668759  1.594842

-3.156485 3.191137

3.165506  -3.999838

-2.786837 -3.099354

4.208187  2.984927

-2.123337 2.943366

0.704199  -0.479481

-0.392370 -3.963704

2.831667  1.574018

-0.790153 3.343144

2.943496  -3.357075

 

2.2 python代码实现

2.2.1 利用numpy手动实现

from numpy import *

#加载数据

def loadDataSet(fileName):

    dataMat = []

    fr = open(fileName)

    for line in fr.readlines():

        curLine = line.strip().split(' ')

        fltLine = map(float, curLine)    #变成float类型

        dataMat.append(fltLine)

    return dataMat

 

# 计算欧几里得距离

def distEclud(vecA, vecB):

    return sqrt(sum(power(vecA - vecB, 2)))

 

#构建聚簇中心，取k个(此例中为4)随机质心

def randCent(dataSet, k):

    n = shape(dataSet)[1]

    centroids = mat(zeros((k,n)))   #每个质心有n个坐标值，总共要k个质心

    for j in range(n):

        minJ = min(dataSet[:,j])

        maxJ = max(dataSet[:,j])

        rangeJ = float(maxJ - minJ)

        centroids[:,j] = minJ + rangeJ * random.rand(k, 1)

    return centroids

 

#k-means 聚类算法

def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):

    m = shape(dataSet)[0]

    clusterAssment = mat(zeros((m,2)))    #用于存放该样本属于哪类及质心距离

    centroids = createCent(dataSet, k)

    clusterChanged = True

    while clusterChanged:

        clusterChanged = False;

        for i in range(m):

            minDist = inf; minIndex = -1;

            for j in range(k):

                distJI = distMeans(centroids[j,:], dataSet[i,:])

                if distJI < minDist:

                    minDist = distJI; minIndex = j

            if clusterAssment[i,0] != minIndex: clusterChanged = True;

            clusterAssment[i,:] = minIndex,minDist**2

        print centroids

        for cent in range(k):

            ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]]   # 去第一列等于cent的所有列

            centroids[cent,:] = mean(ptsInClust, axis = 0)

    return centroids, clusterAssment

 

 

 

2.2.2 利用scikili库实现

Scikit-Learn是基于python的机器学习模块，基于BSD开源许可证。

scikit-learn的基本功能主要被分为六个部分，分类，回归，聚类，数据降维，模型选择，数据预处理。包括SVM，决策树，GBDT，KNN，KMEANS等等

Kmeans在scikit包中即已有实现，只要将数据按照算法要求处理好，传入相应参数，即可直接调用其kmeans函数进行聚类

#################################################

# kmeans: k-means cluster

#################################################

from numpy import *

import time

import matplotlib.pyplot as plt

## step 1:加载数据

print "step 1: load data..."

dataSet = []

fileIn = open('E:/Python/ml-data/kmeans/testSet.txt')

for line in fileIn.readlines():

lineArr = line.strip().split(' ')

dataSet.append([float(lineArr[0]), float(lineArr[1])])

## step 2: 聚类

print "step 2: clustering..."

dataSet = mat(dataSet)

k = 4

centroids, clusterAssment = kmeans(dataSet, k)

## step 3:显示结果

print "step 3: show the result..."

showCluster(dataSet, k, centroids, clusterAssment)

2.2.3 运行结果

不同的类用不同的颜色来表示，其中的大菱形是对应类的均值质心点。

 

 

3、Kmeans算法补充

3.1 kmeans算法缺点

k-means算法比较简单，但也有几个比较大的缺点：

 

（1）k值的选择是用户指定的，不同的k得到的结果会有挺大的不同，如下图所示，左边是k=3的结果，这个就太稀疏了，蓝色的那个簇其实是可以再划分成两个簇的。而右图是k=5的结果，可以看到红色菱形和蓝色菱形这两个簇应该是可以合并成一个簇的：

 

 

 

 

 

 

（2）对k个初始质心的选择比较敏感，容易陷入局部最小值。例如，我们上面的算法运行的时候，有可能会得到不同的结果，如下面这两种情况。K-means也是收敛了，只是收敛到了局部最小值：

 

 

 

（3）存在局限性，如下面这种非球状的数据分布就搞不定了：

 

 

（4）数据集比较大的时候，收敛会比较慢。

 

 

3.2 改良思路

k-means老早就出现在江湖了。所以以上的这些不足也已有了对应方法进行了某种程度上的改良。例如：

ü 问题（1）对k的选择可以先用一些算法分析数据的分布，如重心和密度等，然后选择合适的k

ü 问题（2），有人提出了另一个成为二分k均值（bisecting k-means）算法，它对初始的k个质心的选择就不太敏感