一、简介
二叉树是树这种数据结构的一员,后面我们还会介绍红黑树,2-3-4树等数据结构。那么为什么要使用树?它有什么优点?
前面我们介绍数组的数据结构,我们知道对于有序数组,查找很快,并介绍可以通过二分法查找,但是想要在有序数组中插入一个数据项,就必须先找到插入数据项的位置,然后将所有插入位置后面的数据项全部向后移动一位,来给新数据腾出空间,平均来讲要移动N/2次,这是很费时的。同理,删除数据也是。
然后我们介绍了另外一种数据结构——链表,链表的插入和删除很快,我们只需要改变一些引用值就行了,但是查找数据却很慢了,因为不管我们查找什么数据,都需要从链表的第一个数据项开始,遍历到找到所需数据项为止,这个查找也是平均需要比较N/2次。
那么我们就希望一种数据结构能同时具备数组查找快的优点以及链表插入和删除快的优点,于是树诞生了。
二、树
树(tree)是一种抽象数据类型(ADT),用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点通过连接它们的边组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
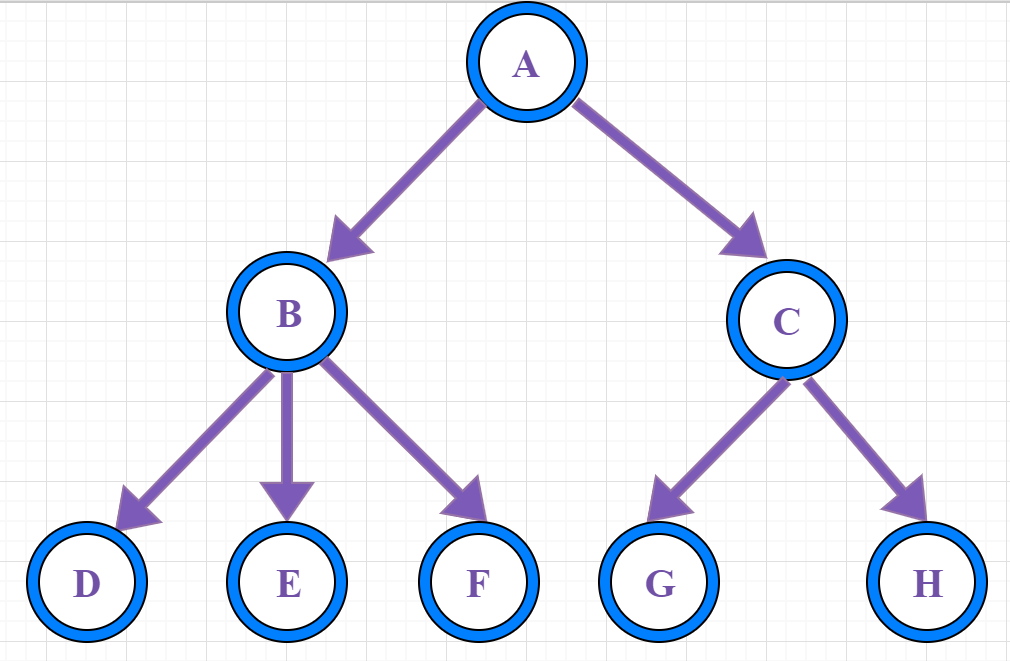
①、节点:上图的圆圈,比如A,B,C等都是表示节点。节点一般代表一些实体,在java面向对象编程中,节点一般代表对象。
②、边:连接节点的线称为边,边表示节点的关联关系。一般从一个节点到另一个节点的唯一方法就是沿着一条顺着有边的道路前进。在Java当中通常表示引用。
树有很多种,向上面的一个节点有多余两个的子节点的树,称为多路树,后面会讲解2-3-4树和外部存储都是多路树的例子。而每个节点最多只能有两个子节点的一种形式称为二叉树,这也是本篇博客讲解的重点。
树的常用术语
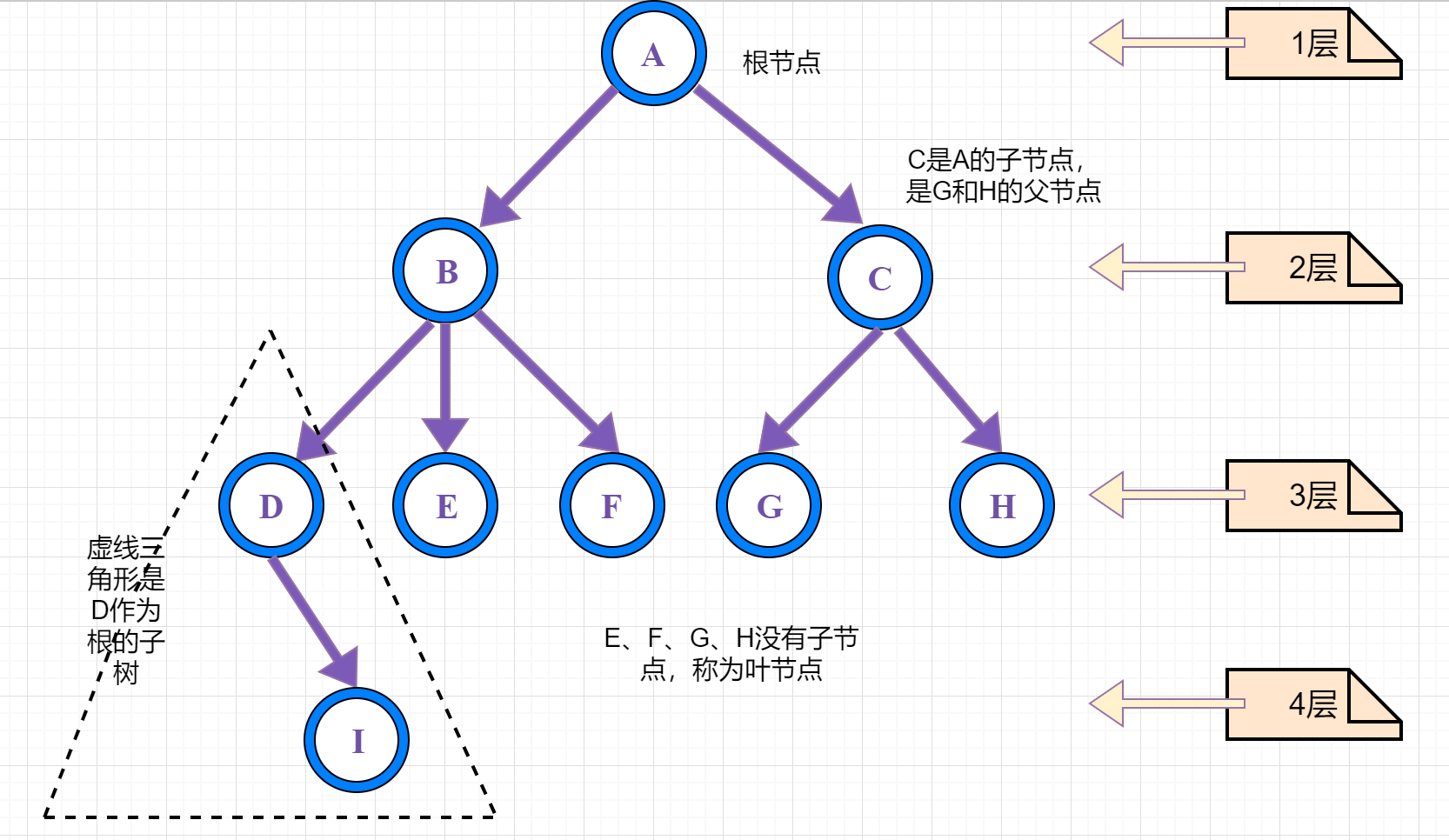
①、路径:顺着节点的边从一个节点走到另一个节点,所经过的节点的顺序排列就称为“路径”。
②、根:树顶端的节点称为根。一棵树只有一个根,如果要把一个节点和边的集合称为树,那么从根到其他任何一个节点都必须有且只有一条路径。A是根节点。
③、父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;B是D的父节点。
④、子节点:一个节点含有的子树的根节点称为该节点的子节点;D是B的子节点。
⑤、兄弟节点:具有相同父节点的节点互称为兄弟节点;比如上图的D和E就互称为兄弟节点。
⑥、叶节点:没有子节点的节点称为叶节点,也叫叶子节点,比如上图的A、E、F、G都是叶子节点。
⑦、子树:每个节点都可以作为子树的根,它和它所有的子节点、子节点的子节点等都包含在子树中。
⑧、节点的层次:从根开始定义,根为第一层,根的子节点为第二层,以此类推。
⑨、深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;
⑩、高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;
三、二叉树
二叉树:树的每个节点最多只能有两个子节点
上图的第一幅图B节点有DEF三个子节点,就不是二叉树,称为多路树;而第二幅图每个节点最多只有两个节点,是二叉树,并且二叉树的子节点称为“左子节点”和“右子节点”。上图的D,E分别是B的左子节点和右子节点。
如果我们给二叉树加一个额外的条件,就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。
二叉搜索树要求:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。

二叉搜索树作为一种数据结构,那么它是如何工作的呢?它查找一个节点,插入一个新节点,以及删除一个节点,遍历树等工作效率如何,下面我们来一一介绍。
二叉树的节点类:
package com.ys.tree; public class Node { private Object data; //节点数据 private Node leftChild; //左子节点的引用 private Node rightChild; //右子节点的引用 //打印节点内容 public void display(){ System.out.println(data); } }
二叉树的具体方法:
package com.ys.tree; public interface Tree { //查找节点 public Node find(Object key); //插入新节点 public boolean insert(Object key); //删除节点 public boolean delete(Object key); //Other Method...... }
四、查找节点
查找某个节点,我们必须从根节点开始遍历。
①、查找值比当前节点值大,则搜索右子树;
②、查找值等于当前节点值,停止搜索(终止条件);
③、查找值小于当前节点值,则搜索左子树;
//查找节点 public Node find(int key) { Node current = root; while(current != null){ if(current.data > key){//当前值比查找值大,搜索左子树 current = current.leftChild; }else if(current.data < key){//当前值比查找值小,搜索右子树 current = current.rightChild; }else{ return current; } } return null;//遍历完整个树没找到,返回null }
用变量current来保存当前查找的节点,参数key是要查找的值,刚开始查找将根节点赋值到current。接在在while循环中,将要查找的值和current保存的节点进行对比。如果key小于当前节点,则搜索当前节点的左子节点,如果大于,则搜索右子节点,如果等于,则直接返回节点信息。当整个树遍历完全,即current == null,那么说明没找到查找值,返回null。
树的效率:查找节点的时间取决于这个节点所在的层数,每一层最多有2n-1个节点,总共N层共有2n-1个节点,那么时间复杂度为O(logn),底数为2。
五、插入节点
要插入节点,必须先找到插入的位置。与查找操作相似,由于二叉搜索树的特殊性,待插入的节点也需要从根节点开始进行比较,小于根节点则与根节点左子树比较,反之则与右子树比较,直到左子树为空或右子树为空,则插入到相应为空的位置,在比较的过程中要注意保存父节点的信息 及 待插入的位置是父节点的左子树还是右子树,才能插入到正确的位置。
//插入节点 public boolean insert(int data) { Node newNode = new Node(data); if(root == null){//当前树为空树,没有任何节点 root = newNode; return true; }else{ Node current = root; Node parentNode = null; while(current != null){ parentNode = current; if(current.data > data){//当前值比插入值大,搜索左子节点 current = current.leftChild; if(current == null){//左子节点为空,直接将新值插入到该节点 parentNode.leftChild = newNode; return true; } }else{ current = current.rightChild; if(current == null){//右子节点为空,直接将新值插入到该节点 parentNode.rightChild = newNode; return true; } } } } return false; }
六、遍历树
遍历树是根据一种特定的顺序访问树的每一个节点。比较常用的有前序遍历,中序遍历和后序遍历。而二叉搜索树最常用的是中序遍历。
①、中序遍历:左子树——》根节点——》右子树
②、前序遍历:根节点——》左子树——》右子树
③、后序遍历:左子树——》右子树——》根节点
//中序遍历 public void infixOrder(Node current){ if(current != null){ infixOrder(current.leftChild); System.out.print(current.data+" "); infixOrder(current.rightChild); } } //前序遍历 public void preOrder(Node current){ if(current != null){ System.out.print(current.data+" "); preOrder(current.leftChild); preOrder(current.rightChild); } } //后序遍历 public void postOrder(Node current){ if(current != null){ postOrder(current.leftChild); postOrder(current.rightChild); System.out.print(current.data+" "); } }
七、查找最大值和最小值
这没什么好说的,要找最小值,先找根的左节点,然后一直找这个左节点的左节点,直到找到没有左节点的节点,那么这个节点就是最小值。同理要找最大值,一直找根节点的右节点,直到没有右节点,则就是最大值。
//找到最大值 public Node findMax(){ Node current = root; Node maxNode = current; while(current != null){ maxNode = current; current = current.rightChild; } return maxNode; } //找到最小值 public Node findMin(){ Node current = root; Node minNode = current; while(current != null){ minNode = current; current = current.leftChild; } return minNode; }
八、删除节点
删除节点是二叉搜索树中最复杂的操作,删除的节点有三种情况,前两种比较简单,但是第三种却很复杂。
1、该节点是叶节点(没有子节点)
2、该节点有一个子节点
3、该节点有两个子节点
下面我们分别对这三种情况进行讲解。
①、删除没有子节点的节点
要删除叶节点,只需要改变该节点的父节点引用该节点的值,即将其引用改为 null 即可。要删除的节点依然存在,但是它已经不是树的一部分了,由于Java语言的垃圾回收机制,我们不需要非得把节点本身删掉,一旦Java意识到程序不在与该节点有关联,就会自动把它清理出存储器。
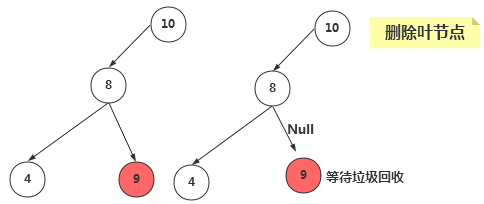
@Override public boolean delete(int key) { Node current = root; Node parent = root; boolean isLeftChild = false; //查找删除值,找不到直接返回false while(current.data != key){ parent = current; if(current.data > key){ isLeftChild = true; current = current.leftChild; }else{ isLeftChild = false; current = current.rightChild; } if(current == null){ return false; } } //如果当前节点没有子节点 if(current.leftChild == null && current.rightChild == null){ if(current == root){ root = null; }else if(isLeftChild){ parent.leftChild = null; }else{ parent.rightChild = null; } return true; } return false; }
删除节点,我们要先找到该节点,并记录该节点的父节点。在检查该节点是否有子节点。如果没有子节点,接着检查其是否是根节点,如果是根节点,只需要将其设置为null即可。如果不是根节点,是叶节点,那么断开父节点和其的关系即可。
②、删除有一个子节点的节点
删除有一个子节点的节点,我们只需要将其父节点原本指向该节点的引用,改为指向该节点的子节点即可。
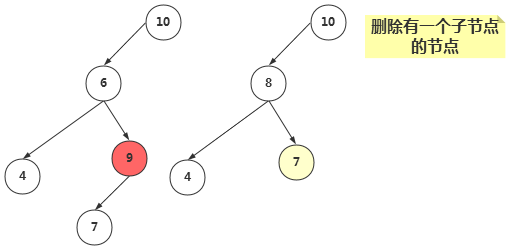
//当前节点有一个子节点 if(current.leftChild == null && current.rightChild != null){ if(current == root){ root = current.rightChild; }else if(isLeftChild){ parent.leftChild = current.rightChild; }else{ parent.rightChild = current.rightChild; } return true; }else{ //current.leftChild != null && current.rightChild == null if(current == root){ root = current.leftChild; }else if(isLeftChild){ parent.leftChild = current.leftChild; }else{ parent.rightChild = current.leftChild; } return true; }
③、删除有两个子节点的节点
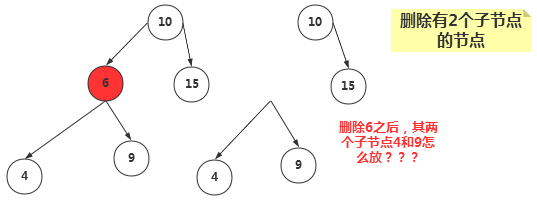
当删除的节点存在两个子节点,那么删除之后,两个子节点的位置我们就没办法处理了。既然处理不了,我们就想到一种办法,用另一个节点来代替被删除的节点,那么用哪一个节点来代替呢?
我们知道二叉搜索树中的节点是按照关键字来进行排列的,某个节点的关键字次高节点是它的中序遍历后继节点。用后继节点来代替删除的节点,显然该二叉搜索树还是有序的。(这里用后继节点代替,如果该后继节点自己也有子节点,我们后面讨论。)
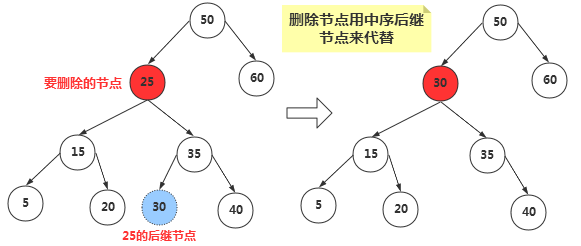
那么如何找到删除节点的中序后继节点呢?其实我们稍微分析,这实际上就是要找比删除节点关键值大的节点集合中最小的一个节点,只有这样代替删除节点后才能满足二叉搜索树的特性。
后继节点也就是:比删除节点大的最小节点。
算法:程序找到删除节点的右节点,(注意这里前提是删除节点存在左右两个子节点,如果不存在则是删除情况的前面两种),然后转到该右节点的左子节点,依次顺着左子节点找下去,最后一个左子节点即是后继节点;如果该右节点没有左子节点,那么该右节点便是后继节点。
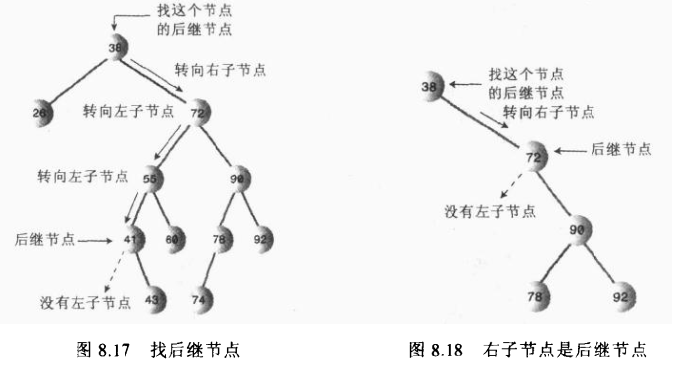
需要确定后继节点没有子节点,如果后继节点存在子节点,那么又要分情况讨论了。
①、后继节点是删除节点的右子节点
这种情况简单,只需要将后继节点表示的子树移到被删除节点的位置即可!
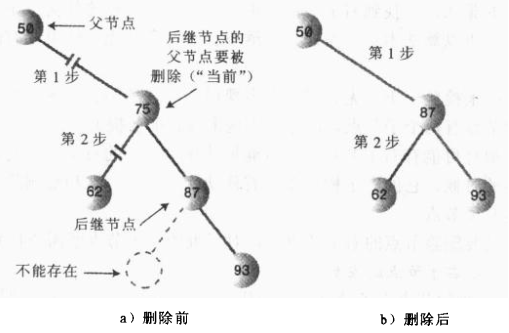
②、后继节点是删除节点的右子节点的左子节点
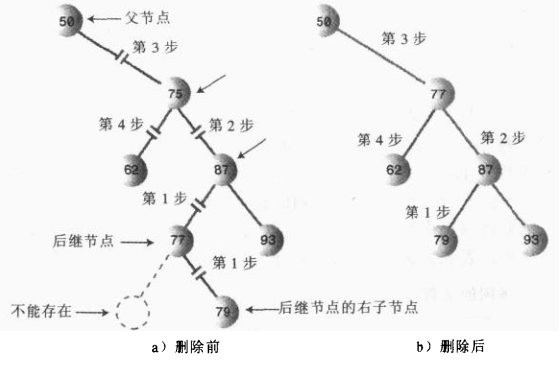
public Node getSuccessor(Node delNode){ Node successorParent = delNode; Node successor = delNode; Node current = delNode.rightChild; while(current != null){ successorParent = successor; successor = current; current = current.leftChild; } //将后继节点替换删除节点 if(successor != delNode.rightChild){ successorParent.leftChild = successor.rightChild; successor.rightChild = delNode.rightChild; } return successor; }
④、删除有必要吗?
通过上面的删除分类讨论,我们发现删除其实是挺复杂的,那么其实我们可以不用真正的删除该节点,只需要在Node类中增加一个标识字段isDelete,当该字段为true时,表示该节点已经删除,反正没有删除。那么我们在做比如find()等操作的时候,要先判断isDelete字段是否为true。这样删除的节点并不会改变树的结构。
public class Node { int data; //节点数据 Node leftChild; //左子节点的引用 Node rightChild; //右子节点的引用 boolean isDelete;//表示节点是否被删除 }
九、二叉树的效率
从前面的大部分对树的操作来看,都需要从根节点到下一层一层的查找。
一颗满树,每层节点数大概为2n-1,那么最底层的节点个数比树的其它节点数多1,因此,查找、插入或删除节点的操作大约有一半都需要找到底层的节点,另外四分之一的节点在倒数第二层,依次类推。
总共N层共有2n-1个节点,那么时间复杂度为O(logn),底数为2。
在有1000000 个数据项的无序数组和链表中,查找数据项平均会比较500000 次,但是在有1000000个节点的二叉树中,只需要20次或更少的比较即可。
有序数组可以很快的找到数据项,但是插入数据项的平均需要移动 500000 次数据项,在 1000000 个节点的二叉树中插入数据项需要20次或更少比较,在加上很短的时间来连接数据项。
同样,从 1000000 个数据项的数组中删除一个数据项平均需要移动 500000 个数据项,而在 1000000 个节点的二叉树中删除节点只需要20次或更少的次数来找到他,然后在花一点时间来找到它的后继节点,一点时间来断开节点以及连接后继节点。
所以,树对所有常用数据结构的操作都有很高的效率。
遍历可能不如其他操作快,但是在大型数据库中,遍历是很少使用的操作,它更常用于程序中的辅助算法来解析算术或其它表达式。
十、用数组表示树
用数组表示树,那么节点是存在数组中的,节点在数组中的位置对应于它在树中的位置。下标为 0 的节点是根,下标为 1 的节点是根的左子节点,以此类推,按照从左到右的顺序存储树的每一层。
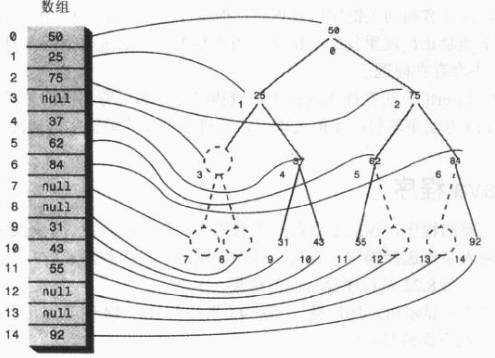
树中的每个位置,无论是否存在节点,都对应于数组中的一个位置,树中没有节点的在数组中用0或者null表示。
假设节点的索引值为index,那么节点的左子节点是 2*index+1,节点的右子节点是 2*index+2,它的父节点是 (index-1)/2。
在大多数情况下,使用数组表示树效率是很低的,不满的节点和删除掉的节点都会在数组中留下洞,浪费存储空间。更坏的是,删除节点如果要移动子树的话,子树中的每个节点都要移到数组中新的位置,这是很费时的。
不过如果不允许删除操作,数组表示可能会很有用,尤其是因为某种原因要动态的为每个字节分配空间非常耗时。
十一、完整的BinaryTree代码
Node.java
package com.ys.tree; public class Node { int data; //节点数据 Node leftChild; //左子节点的引用 Node rightChild; //右子节点的引用 boolean isDelete;//表示节点是否被删除 public Node(int data){ this.data = data; } //打印节点内容 public void display(){ System.out.println(data); } }
Tree.java
package com.ys.tree; public interface Tree { //查找节点 public Node find(int key); //插入新节点 public boolean insert(int data); //中序遍历 public void infixOrder(Node current); //前序遍历 public void preOrder(Node current); //后序遍历 public void postOrder(Node current); //查找最大值 public Node findMax(); //查找最小值 public Node findMin(); //删除节点 public boolean delete(int key); //Other Method...... }
BinaryTree.java
package com.ys.tree; public class BinaryTree implements Tree { //表示根节点 private Node root; //查找节点 public Node find(int key) { Node current = root; while(current != null){ if(current.data > key){//当前值比查找值大,搜索左子树 current = current.leftChild; }else if(current.data < key){//当前值比查找值小,搜索右子树 current = current.rightChild; }else{ return current; } } return null;//遍历完整个树没找到,返回null } //插入节点 public boolean insert(int data) { Node newNode = new Node(data); if(root == null){//当前树为空树,没有任何节点 root = newNode; return true; }else{ Node current = root; Node parentNode = null; while(current != null){ parentNode = current; if(current.data > data){//当前值比插入值大,搜索左子节点 current = current.leftChild; if(current == null){//左子节点为空,直接将新值插入到该节点 parentNode.leftChild = newNode; return true; } }else{ current = current.rightChild; if(current == null){//右子节点为空,直接将新值插入到该节点 parentNode.rightChild = newNode; return true; } } } } return false; } //中序遍历 public void infixOrder(Node current){ if(current != null){ infixOrder(current.leftChild); System.out.print(current.data+" "); infixOrder(current.rightChild); } } //前序遍历 public void preOrder(Node current){ if(current != null){ System.out.print(current.data+" "); infixOrder(current.leftChild); infixOrder(current.rightChild); } } //后序遍历 public void postOrder(Node current){ if(current != null){ infixOrder(current.leftChild); infixOrder(current.rightChild); System.out.print(current.data+" "); } } //找到最大值 public Node findMax(){ Node current = root; Node maxNode = current; while(current != null){ maxNode = current; current = current.rightChild; } return maxNode; } //找到最小值 public Node findMin(){ Node current = root; Node minNode = current; while(current != null){ minNode = current; current = current.leftChild; } return minNode; } @Override public boolean delete(int key) { Node current = root; Node parent = root; boolean isLeftChild = false; //查找删除值,找不到直接返回false while(current.data != key){ parent = current; if(current.data > key){ isLeftChild = true; current = current.leftChild; }else{ isLeftChild = false; current = current.rightChild; } if(current == null){ return false; } } //如果当前节点没有子节点 if(current.leftChild == null && current.rightChild == null){ if(current == root){ root = null; }else if(isLeftChild){ parent.leftChild = null; }else{ parent.rightChild = null; } return true; //当前节点有一个子节点,右子节点 }else if(current.leftChild == null && current.rightChild != null){ if(current == root){ root = current.rightChild; }else if(isLeftChild){ parent.leftChild = current.rightChild; }else{ parent.rightChild = current.rightChild; } return true; //当前节点有一个子节点,左子节点 }else if(current.leftChild != null && current.rightChild == null){ if(current == root){ root = current.leftChild; }else if(isLeftChild){ parent.leftChild = current.leftChild; }else{ parent.rightChild = current.leftChild; } return true; }else{ //当前节点存在两个子节点 Node successor = getSuccessor(current); if(current == root){ successor = root; }else if(isLeftChild){ parent.leftChild = successor; }else{ parent.rightChild = successor; } successor.leftChild = current.leftChild; } return false; } public Node getSuccessor(Node delNode){ Node successorParent = delNode; Node successor = delNode; Node current = delNode.rightChild; while(current != null){ successorParent = successor; successor = current; current = current.leftChild; } //后继节点不是删除节点的右子节点,将后继节点替换删除节点 if(successor != delNode.rightChild){ successorParent.leftChild = successor.rightChild; successor.rightChild = delNode.rightChild; } return successor; } public static void main(String[] args) { BinaryTree bt = new BinaryTree(); bt.insert(50); bt.insert(20); bt.insert(80); bt.insert(10); bt.insert(30); bt.insert(60); bt.insert(90); bt.insert(25); bt.insert(85); bt.insert(100); bt.delete(10);//删除没有子节点的节点 bt.delete(30);//删除有一个子节点的节点 bt.delete(80);//删除有两个子节点的节点 System.out.println(bt.findMax().data); System.out.println(bt.findMin().data); System.out.println(bt.find(100)); System.out.println(bt.find(200)); } }
十二、总结
树是由边和节点构成,根节点是树最顶端的节点,它没有父节点;二叉树中,最多有两个子节点;某个节点的左子树每个节点都比该节点的关键字值小,右子树的每个节点都比该节点的关键字值大,那么这种树称为二叉搜索树,其查找、插入、删除的时间复杂度都为logN;可以通过前序遍历、中序遍历、后序遍历来遍历树,前序是根节点-左子树-右子树,中序是左子树-根节点-右子树,后序是左子树-右子树-根节点;删除一个节点只需要断开指向它的引用即可;哈夫曼树是二叉树,用于数据压缩算法,最经常出现的字符编码位数最少,很少出现的字符编码位数多一些。
十三、扩展
非递归遍历二叉树
// 非递归遍历(思路很简单,先准备好当前行数据并打印,同时准备好下一行数据,再让当前指针指向下一行,如此循环,直到下一行没有数据退出循环) public static void noRecursionOrder(Node rootNode){ List<Node> linelist = new ArrayList<>(); linelist.add(rootNode); while (true) { if (linelist != null && linelist.size() > 0) { List<Node> nextlinelist = new ArrayList<>(); for (int i = 0; i < linelist.size(); i++) { Node currentNode = linelist.get(i); System.out.println(currentNode.data); if (currentNode.getLeftChild() != null) { nextlinelist.add(currentNode.getLeftChild()); } if (currentNode.getRightChild() != null) { nextlinelist.add(currentNode.getRightChild()); } } if (nextlinelist.size()<=0) { break; }else{ linelist = nextlinelist; } } } }
按层次打印二叉树
有一棵二叉树,请设计一个算法,按照层次打印这棵二叉树。
给定二叉树的根结点root,请返回打印结果,结果按照每一层一个数组进行储存,所有数组的顺序按照层数从上往下,且每一层的数组内元素按照从左往右排列。保证结点数小于等于500。
// 思路很简单,每次当前行元素加进数组后,准备好下一行的所有元素(放到一个集合里),依次递归 public static void lineByLinePrint(Node root){ if (root != null) { Node[] currentNodes = {root}; while (true) { List<Node> nextnodelist = new ArrayList<>(); if (currentNodes != null && currentNodes.length>0) { // 遍历打印当前行,并且准备下一行节点 for (int i = 0; i < currentNodes.length; i++) { if (currentNodes[i] != null && currentNodes[i].data != null && !"".equals(currentNodes[i].data)) { System.out.print(currentNodes[i].data+" "); if (currentNodes[i].getLeftChild() != null) { nextnodelist.add(currentNodes[i].getLeftChild()); } if (currentNodes[i].getRightChild() != null) { nextnodelist.add(currentNodes[i].getRightChild()); } } } } // 下一行有节点就指针转向下一行,没有就退出循环 if (nextnodelist.size()>0) { currentNodes = nextnodelist.toArray(new Node[nextnodelist.size()]); }else{ break; } System.out.println(); } } }
二叉树的序列化练习题
首先我们介绍二叉树先序序列化的方式,假设序列化的结果字符串为str,初始时str等于空字符串。先序遍历二叉树,如果遇到空节点,就在str的末尾加上“#!”,“#”表示这个节点为空,节点值不存在,当然你也可以用其他的特殊字符,“!”表示一个值的结束。如果遇到不为空的节点,假设节点值为3,就在str的末尾加上“3!”。现在请你实现树的先序序列化。
给定树的根结点root,请返回二叉树序列化后的字符串。
判断一个二叉树是否是完全二叉树
提示:层序遍历变型题。
(1)基础知识
【二叉树】:二叉树是一棵特殊的树,二叉树每个节点最多有两个孩子结点,分别称为左孩子和右孩子。
【满二叉树】:高度为N的满二叉树有2^N- 1个节点的二叉树。
【完全二叉树】: 若设二叉树的深度为h,除第h 层外,其它各层(1~h-1) 的结点数都达到最大个数,第h 层所有的结点都连续集中在最左边,这就是完全二叉树
【满二叉树是完全二叉树的特例】
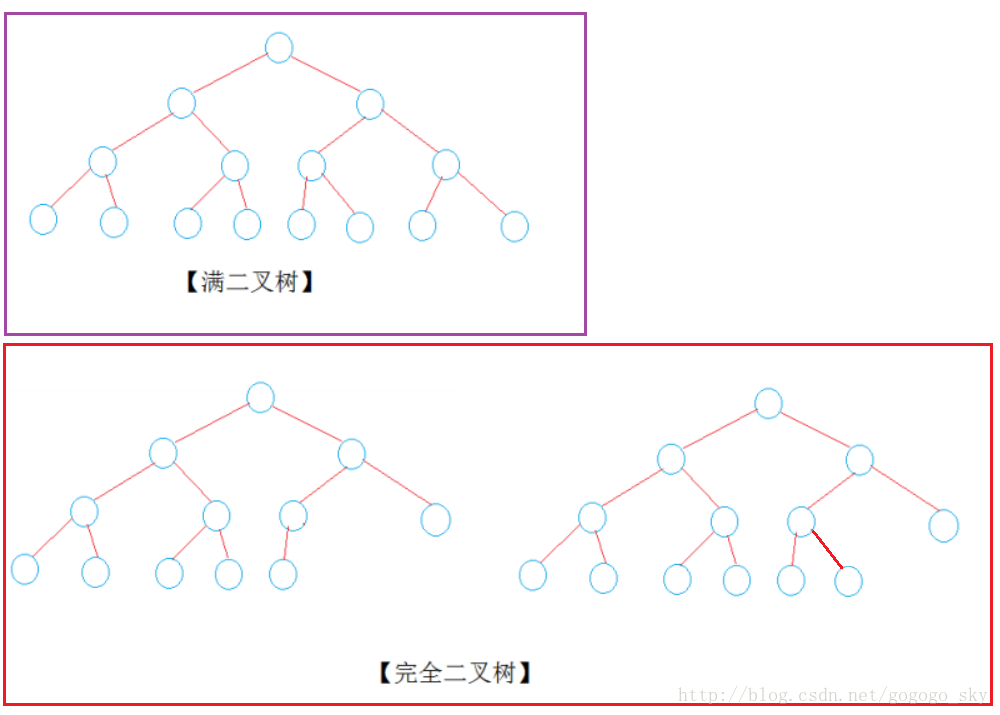
(2)判断一棵树是否是完全二叉树的思路
1>如果树为空,则直接返回错
2>如果树不为空:层序遍历二叉树
2.1>如果一个结点左右孩子都不为空,则pop该节点,将其左右孩子入队列;
2.1>如果遇到一个结点,左孩子为空,右孩子不为空,则该树一定不是完全二叉树;
2.2>如果遇到一个结点,左孩子不为空,右孩子为空;或者左右孩子都为空;则该节点之后的队列中的结点都为叶子节点;该树才是完全二叉树,否则就不是完全二叉树;
public boolean isComplete(TreeNode root){ boolean result = false; boolean leaf = false;// true 需要判断是否是叶子节点,也就是说前面出现过左节点不为空的情况, false 不需要考虑这种情况 if (root != null) { List<TreeNode> linelist = new ArrayList();// 当前层的节点集合 linelist.add(root); Mark_x:while (true) { List<TreeNode> nextlinelist = new ArrayList(); if (linelist.size() > 0) { for (int i = 0; i < linelist.size(); i++) { TreeNode currentNode = linelist.get(i); if (leaf) {// 只要出现一个非叶子节点,就再置为false if (currentNode.getLeftChild() != null || currentNode.getRightChild() != null) { result = false; leaf = false; } } if(leaf==false){ // 左右节点都不为空,继续下个节点 if (currentNode.getLeftChild() != null && currentNode.getRightChild() != null) { } // 左节点为空,右节点不为空,肯定不是完全二叉树 if (currentNode.getLeftChild() == null && currentNode.getRightChild() != null) { result = false; break Mark_x; } // 左节点不为空,右节点为空或左右节点都为空,继续观察后续节点是不是都是叶子节点 if ((currentNode.getLeftChild() != null && currentNode.getRightChild() == null) || (currentNode.getLeftChild() == null && currentNode.getRightChild() == null)) { result = true; leaf = true; } } } // 准备下一层节点 for (int i = 0; i < linelist.size(); i++) { if (linelist.get(i).getLeftChild() != null) { nextlinelist.add(linelist.get(i).getLeftChild()); } if (linelist.get(i).getRightChild() != null) { nextlinelist.add(linelist.get(i).getRightChild()); } } if (nextlinelist.size()<=0) { break; }else{ linelist = nextlinelist; } } } } return result; }
判断一个二叉树是否是满二叉树
寻找错误结点练习题
一棵二叉树原本是搜索二叉树,但是其中有两个节点调换了位置,使得这棵二叉树不再是搜索二叉树,请找到这两个错误节点并返回他们的值。保证二叉树中结点的值各不相同。给定一棵树的根结点,请返回两个调换了位置的值,其中小的值在前。
分析
根据搜索二叉树的性质可知
1、搜索二叉树进行中序遍历,依次出现的节点值会一直升序,如果出现降序,则有结点位置被置换了;
2、如果在中序遍历时结点值出现了两次降序,第一个错误结点为第一次降序时较大的结点,第二个错误的结点为第二次降序时较小的结点;
3、如果在中序遍历时结点值只出现了一次降序,第一个错误的结点为这次降序时较大的结点,第二个错误的结点为这次降序时较小的结点。
代码实现
/** * 一棵二叉树原本是搜索二叉树,但是其中有两个节点调换了位置, * 使得这棵二叉树不再是搜索二叉树,请找到这两个错误节点并返回他们的值。保证二叉树中结点的值各不相同。 * 给定一棵树的根结点,请返回两个调换了位置的值,其中小的值在前。 */ private class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } private int[] findError(TreeNode root) { // write code here int[] res = new int[2]; ArrayDeque<TreeNode> queue = new ArrayDeque(); TreeNode cur=root; TreeNode point=null;//栈顶弹出的元素,是用来比较的第一个元素 while (!queue.isEmpty() || cur != null) { if (cur != null) { queue.addLast(cur); cur = cur.left; } else { cur = queue.pollLast(); if (point != null && point.val > cur.val) { res[1] = res[1] == 0 ? point.val : res[1]; res[0] = cur.val; } point = cur; cur = cur.right; } } return res; }
树上最远距离练习题
从二叉树的节点A出发,可以向上或者向下走,但沿途的节点只能经过一次,当到达节点B时,路径上的节点数叫作A到B的距离。对于给定的一棵二叉树,求整棵树上节点间的最大距离。给定一个二叉树的头结点root,请返回最大距离。保证点数大于等于2小于等于500.
思路:理解题目的含义,对于一棵以root为根的二叉树,树上的最大距离可能来自3中情况:
情况1:完全来自root的左子树,如图所示,即最大路径不经过root结点,只在结点1的左子树2上面,此时的最大距离为8。
情况2:完全来自root结点的右子树,如图所示,最大路径不经过root结点,只在结点1的右侧左子树3上面,此时最大距离是9。
情况3:来自结点root的两侧,如图所示,经过root结点,此时的最大距离=root的左子树的高度(即结点3的最长路径)+root右子树的高度(即结点3的最长路径)+root结点本身。
分析可知,要计算结点root所在子树的最长距离,需要已知:左子树②的最长距离LMaxLength,左子树的高度LHeight;右子树③的最长距离RMaxLength,右子树的高度RHeight.然后比较Math.max(LMax,RMax,(LHeight+RHeight+1)),其最大值就是这棵二叉树的最大距离,即对于每个子树,需要求出它的最大距离和最大高度。显然这就是一个递推关系式,可以使用递归来实现,即设计一个递归函数,给定一个根结点root,求出这个根结点的最大距离max和最大高度height并返回这2个数值。其中maxLength= Math.max(LMax,RMax,(LHeight+RHeight+1));而由于要返回这棵子树的高度,如何求子树的高度呢?二叉树的高度就是它的2个子树高度中的较大值再加上1,即height=Math.max(LHeight, RHeight)+1;
递归的递推关系有了,关键是找到递归的起始条件或者理解为终止条件。这里使用的思想是后序遍历(先遍历左右子树再处理结论),联系二叉树的后序遍历算法,进行改编。显然if(root==null)时:max=0;height=0;
总结:设计一个递归函数,输入根结点root,求出这棵二叉树的最大距离maxLength和高度length并返回。递推关系为:
maxLength= Math.max(LMax,RMax,(LHeight+RHeight+1));
height=Math.max(LHeight, RHeight)+1
边界条件为:
if(root==null) return max=0;height=0;
在Java中不能分开返回2个值,因此要将2个值整合成为一个数组进行返回即可。
// 求二叉树上结点的最大距离:递归;最大值只可能来自3中情况 public int findLongest(TreeNode root) { // 特殊输入 if (root == null) return 0; // 调用递归函数来求得最大距离maxLength和高度height int[] results = this.process(root); // 返回结果 return results[0]; } // 这是一个递归方法,用于求出一个二叉树的最大距离和高度并返回这2个值 private int[] process(TreeNode root) { int[] tempResults = new int[2]; // 边界条件 if (root == null) { tempResults[0] = 0; tempResults[1] = 0; return tempResults; } // 最大值来自3中情况,进行比较 // 左子树的结果: int[] paramLeft = this.process(root.getLeftChild()); int LMaxLength = paramLeft[0]; int LHeight = paramLeft[1]; // 右子树的结果: int[] paramRight = this.process(root.getRightChild()); int RMaxLength = paramRight[0]; int RHeight = paramRight[1]; // 比较得到最大值和高度,并组成数组返回,常识:Math.max()函数只能比较2个数的大小 // 递归的递推关系 tempResults[0] = Math.max(Math.max(LMaxLength, RMaxLength), LHeight + RHeight + 1); tempResults[1] = Math.max(LHeight, RHeight) + 1; // 带有返回值的递归函数 return tempResults; }
常识:Math.max()函数只能放入2个参数,即只能比较2个数的大小,如果需要比较更多数的大小,那么在Math.max()里面再套用Math.max()即可。
对于递归方法,可以有返回值也可以没有返回值,并不影响递归的使用,递归的设计应该从功能上来思考,思考这个递归方法需要解决一个什么问题?需要输入的信息是什么?返回的信息又是什么?在这个递归方法中需要对下一层递归方法的返回值进行怎样的处理?(即如何递推);从策略上来讲,就是先明确递推关系再明确初始条件(终止条件)。
最大二叉搜索子树练习题
有一棵二叉树,其中所有节点的值都不一样,找到含有节点最多 的搜索二叉子树,并返回这棵子树的头节点.
给定二叉树的头结点root,请返回所求的头结点,若出现多个节点最多的子树,返回头结点权值最大的。