二进制求和
上次弄了大整数乘法之后后来想了一下用二进制来进行大整数乘法,但是后来看了一下,在计算求和和减法操作时用十进制确实比较省事,但是怎么二进制求和呢?
声明:本文有转载成分,详情请点击以下参考链接:
https://leetcode-cn.com/problems/add-binary/solution/er-jin-zhi-qiu-he-by-leetcode/
https://blog.csdn.net/derrantcm/article/details/47203323
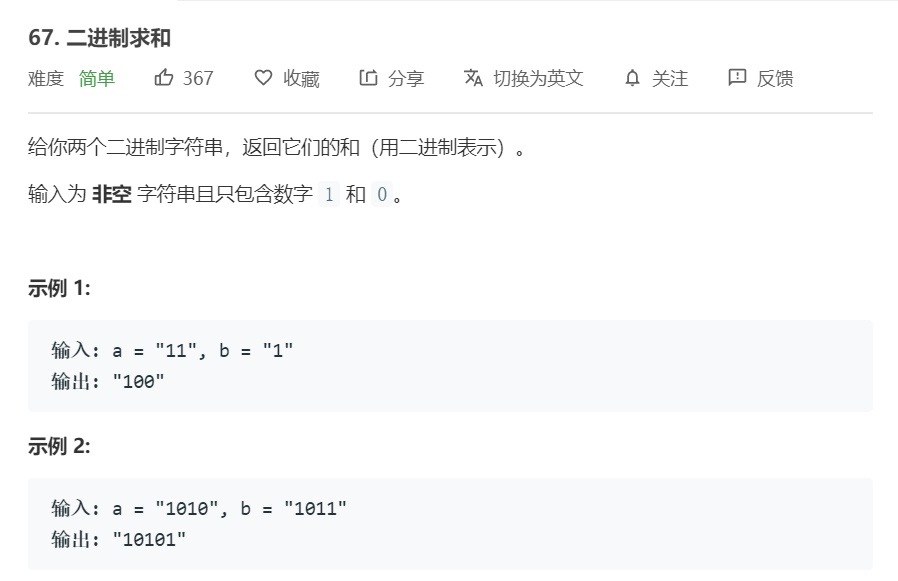
题目描述:
方法一:
class Solution {
public String addBinary(String a, String b) {
return Integer.toBinaryString(Integer.parseInt(a, 2) + Integer.parseInt(b, 2));
}
}
缺点:1:在 Java 中,该方法受输入字符串 a 和 b 的长度限制。字符串长度太大时,不能将其转换为 Integer,Long 或者 BigInteger 类型。
2:如果输入的数字很大,该方法的效率非常低。
算法的时间复杂度为O(N+M)
所以用位计算才能真正提高效率
方法二(逐位计算):
这里注意二进制的和最大也就
撑大一位
package cn.htu.test;
public class Solution {
public static String addBinary(String a, String b) {
//要注意a串和b串长度不一定等哦
int[] ca = new int[a.length()];//ca为存储a串的字符数组
int[] cb = new int[b.length()];//cb为存储b串的字符数组
// 将字符数组中的值转换了数值的0或者1
for (int i = 0; i < a.length(); i++) {
ca[i] = a.charAt(i) - '0';
}
// 将字符数组中的值转换了数值的0或者1
for (int i = 0; i < b.length(); i++) {
cb[i] = b.charAt(i) - '0';
}
// 使用ca保存的长度长(把长的放到ca里来,这样才清楚同一速度下谁先遍历完)
if (ca.length < cb.length) {
int[] tmp = ca;
ca = cb;
cb = tmp;
}
int ai = ca.length - 1; // 字符数组ca最后一个索引下标(即长度减一)
int bi = cb.length - 1; // 字符数组cb最后一个索引下标
int carry = 0; // 下位的进位标识
int result; // 加载的结果
// 计算比如:1010101101 + 10100
while (ai >= 0 && bi >= 0) {
result = ca[ai] + cb[bi] + carry;//result最多也就是3,mod2只有也就是1
ca[ai] = result % 2;//整个算法的关键,后一位的值等于前一位的结果mod2
carry = result / 2;
//carry是0或1,当result=0,1的时候carry为0,不进位,
//当result为2或3的时候carry是1,产生进位
ai--;
bi--;
}
// 处理余下的数字(因为ca较长还有剩余数字)
while (ai >= 0) {
result = ca[ai] + carry;
ca[ai] = result % 2;
carry = result / 2;
if (carry == 0) {//在最后的这一段单独的ca部分数组中,不产生进位就结束了
break;
}
ai--;
}
// 将字符数组中的值转换了字符的0或者1
for (int i = 0; i < ca.length; i++) {
ca[i] += '0';//被字符'0'给亲了就是字符了
}
// 不需要扩展一位,因为两个二进制相加结果最多也就撑大一位
if (carry == 0) {//如果最后没有剩下进位了
char[] ch = new char[ca.length];
for (int i = 0; i < ca.length; i++) {
ch[i] = (char) (ca[i]);
}
return new String(ch);//返回对象
}
// 需要扩展一位
else {
char[] ch = new char[ca.length + 1];
ch[0] = '1';//最高位就是1咯
for (int i = 0; i < ca.length; i++) {
ch[i + 1] = (char) (ca[i]);
}
return new String(ch);
}
}
public static void main(String[] args) {
String aString = "10010001110";
String bString = "10010101";
System.out.println("output:"+addBinary(aString,bString));
}
}
方法三(位运算):
总的来说就是先ab不进位
异或(异或就是异为1,同为0),然后再对ab进行&(&其实我们理解的乘,而不是加,要注意),然后把结果左移一位放到carry里面

import java.math.BigInteger;
class Solution {
public String addBinary(String a, String b) {
BigInteger x = new BigInteger(a, 2);
BigInteger y = new BigInteger(b, 2);
BigInteger zero = new BigInteger("0", 2);
BigInteger carry, answer;
while (y.compareTo(zero) != 0) {
answer = x.xor(y);
carry = x.and(y).shiftLeft(1);
x = answer;
y = carry;
}
return x.toString(2);
}
}
