译文转:https://blog.csdn.net/alihouzi/article/details/45190303
原文转:http://users.rowan.edu/~polikar/WTpart1.html
连续小波变换的计算
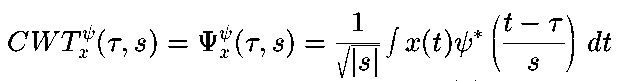
对上面公式的解释将在本节中进行详细说明。以x(t)作为被分析的信号。选用的小波作为信号处理中用到的所有窗函数的原型。应用的所有窗都是母小波的放大(或缩小)和平移版本。有很多函数可以满足这个条件。Morlet小波和墨西哥帽小波(Mexican hat)是其中最有代表性的,本章中后面部分中所举的例子也会用这两个小波进行小波分析。
一旦选择了母小波,就可以从s=1开始计算了,连续小波变换就是计算对应所有值的s,或者小于1,或者大于1。不过,与要分析的信号有关,一般不需要完整的变换。对所有的应用来说,信号是有带宽限制的,因此,在有限时间内做变换就经常能够满足要求了。在这篇文章里的后续部分,只用到s在有限时间内的值。
为方便起见,计算过程将会始于s=1,然后s值逐渐增大,即分析将会从高频开始,然后逐步到低频。s的第一个值是对大多数缩小的小波的反映。随着s增大,小波逐渐被放大。
小波要被放在信号的最初点,即t=0时刻。用尺度为1的小波函数与信号相乘,然后在所有时间内做积分。积分结果再乘上这个常量——1/sqrt(s)。后面这次相乘是为了使能量归一化处理而作的,其目的是使变换后的信号在任意比例上都有相同的能量。最终结果就是变换后的值,即在t=0时刻和s=1的情况下的连续小波变换。换句话说,就是在时间-尺度平面内,tau=0,s=1时刻信号的响应。
然后平移s=1时的小波值至t=tau时刻的位置,得到在时间-尺度平面内,t=tau,s=1时刻信号的响应。
重复这个过程,直到小波到达了信号的末端。这是,在时间-尺度平面内,就会得到一系列的点。
然后,将s增大一点。注意到,这是小波变换,所以tau和s都必须连续的增加。不过,如果是由计算机来进行这个变换过程,两个参数都以一个很小的步长增加。这是由于采样造成的。
对所有s值,重复上面这个过程。每一个根据给定的s计算的结果都对应时间-尺度平面内的一行。当对所应所有的s都计算完成后,对信号的连续小波变换就完成了。
下面的图说明了计算过程的每一步:
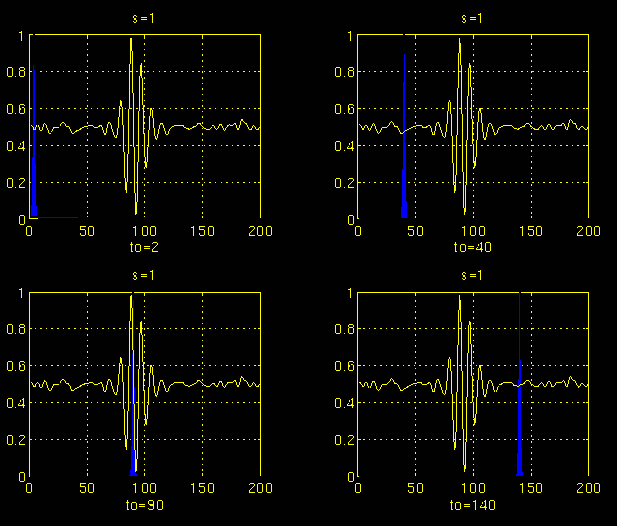
图3.3
在图3.3中,显示了在四个不同时刻tau时的信号和小波函数。信号是图3.1所示的信号的裁剪版本,对应着信号的高频部分。可以看到它多么紧凑(蓝色的窗口)。它的宽度应该与信号中最高频分量出现的时间一致。图中显示了to=2,to=40,to=90和to=140时刻小波的位置。在每一个位置,都将它与信号相乘。很明显,只有在小波的支撑域内,乘积不为0,其余部分全为0。通过在时间轴上平移小波,信号被定位在时间轴上。进一步,通过改变s的值,信号又被定为在频率范围内。
如果信号对当前的s值有一个谱分量(这个例子中s的值是1),在信号的谱分量出现的时刻,信号与小波的乘积会相当大。如果对于当前的s值,谱分量不存在,那么,乘积将会很小或为0。图3.3中,在s=1和t=100ms附近,信号中存在一个窗口宽度的频谱分量。
图3.3中,在100ms时,对信号做连续小波变换后将会产生大的结果,在其他时候则值很小。另一方面,当尺度很高时,连续小波变换将对在整个信号周期内得到一个很大的值,因为低频信号在整个周期内都存在。