本文是对我原先写的python常用序列list、tuples及矩阵库numpy的使用中的numpy矩阵库的使用的补充。结合我个人现在对线性代数的复习进度来不断更博。
- Section 1:行列式的计算
我们知道,线代中,行列式是相当重要的一部分,因为行列式通常决定了一个矩阵的逆是否存在以及方程是否有解等,因此,掌握行列式的计算相当重要,结合numpy矩阵库,对我们所学进行拓展,并且在学习的过程中还能掌握numpy的使用,可谓一举两得。
在原先的博客中,已经提及了numpy中如何创建矩阵、如何求解矩阵的逆以及numpy中一些矩阵的操作运算等。在这一节主要讲解行列式的计算函数det。
在numpy中,带有一个计算行列式值的计算函数,det。它存在于linalg类下,可以通过点操作符来调用。以下面这道行列式值的求解为例:
ex1:
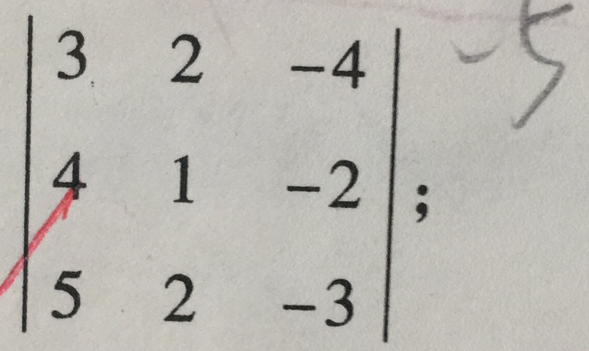
可以看到,我通过手算的值为-5,下面使用numpy库来计算,代码如下:

1 import numpy as np 2 import numpy.linalg as lg 3 4 A = np.array([[3, 2, -4], [4, 1, -2], 5 [5, 2, -3]]) 6 print A 7 8 det_A = lg.det(A) 9 print "The value of det A is :" 10 print det_A
得到的输出结果为:

可以看到与我所算的结果一样。
需要注意的是,numpy矩阵库所带的det函数无法计算元素为字符的矩阵,如下列行列式的值就无法计算:
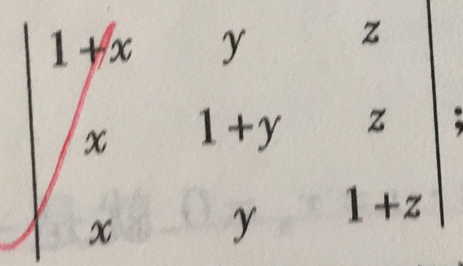
在求解线性方程中,矩阵秩的求解非常重要,它是方程组是否有解的充分必要条件。在numpy中使用线性代数包中的matrix_rank进行求解矩阵的秩,其使用方法如下所示:

1 import numpy as np 2 import numpy.linalg as lg 3 A = np.array([[1, 0, 0, 0], [-2, 3, 0, 0], 4 [0, -4, 5, 0], [0, 0, -6, 7]]) 5 print "The matrix_rank of A: " 6 print lg.matrix_rank(A)
以下面这道题为例,手算的结果为3:
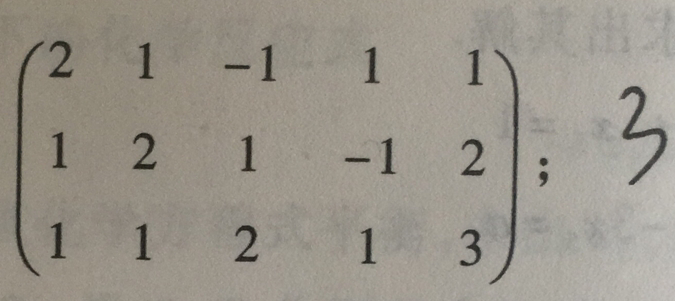
使用上述代码,求得的结果为: