2-3-4树
首先2-3-4树为什么要叫做2-3-4树
因为这棵树除了叶子节点,所有的节点都只有2个孩子或3个孩子或4个孩子。这里所说的叶子结点我们当前默认全是空节点,就类似树的原来的叶子节点的孩子都是空节点,叫这些空节点叶子结点。
就像这样: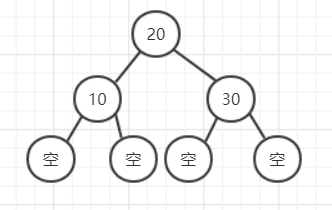
说节点都只有2个孩子或3个孩子或4个孩子,说明节点有3种,
- 第一种是有两个孩子的:
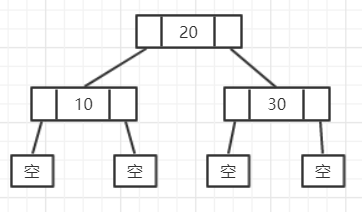
图中的20就是这一种 - 第二种是有3个孩子的:

这里的空节点就先省略了,可见这种节点10和20在一个节点中,但也是按照一定的顺序排列的,并且5连接在10的左边,15连接在10和20中间,25在20右边 - 第三种是有4个孩子的
这种就和第二种很像了,只不过节点中存放了3个值
图中每个值连接的位置依然是有序的
2-3-4树中的非叶子节点就是由这三类节点构成的。
同时2-3-4树还有一个特性是所有的叶子节点的深度都是相同的
这个是什么意思呢?就是所有的空节点的祖先的个数都是相同的,也意味着所有的非叶子结点的孩子必须连满。举个例子:
上面这个图10的左边没有连其他节点,所以它没有连满,也就是10的左边连的是一个空节点,那么这个空节点和15的孩子同样都是空节点,但是祖先的个数却不一样,所以它就不是2-3-4树。这种情况会在节点删除的时候发生,之后就要做一些调整把它重新调整为2-3-4树。
我们接下来介绍一下2-3-4树的插入
2-3-4树的插入
说到插入就要谈到搜索,2-3-4树的搜索其实和二叉搜索树非常相似,说到底它是一颗搜索树,节点还是按照从左到右依次增大的顺序排列的,对于给定的一个搜索值,从根节点出发,挨个比较,向下寻找就可以了。
通过搜索,就可以找到节点插入的位置,但难点在于插入后的调整。
先看一个插入调整的例子(为了简便,里边的节点就不再画成矩形了,也不再画分割线了,空节点也同样省略了,但是连接的位置还是按照顺序的):
插入节点时,首先并不是向下插入,而是先合并到搜索到的位置上,就像是上图中的6,12,15,当插入15后,这个节点中存储了4个值,所以就需要进行调整: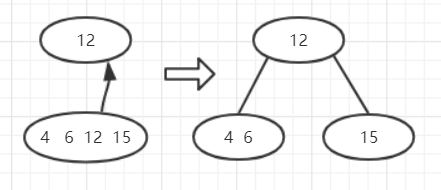
我们把这4个值中的第3个提出来(我觉得把第二个提出来也行),也就是12,让它作为父节点,将原来的节点拆分并按顺序连接到12,我们重新调整为2-3-4树
接下来继续插入其他值: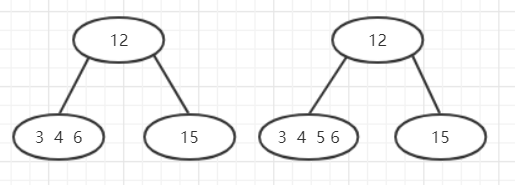
在添加了3和5之后,最左边的节点又变成了异常状态,于是继续调整: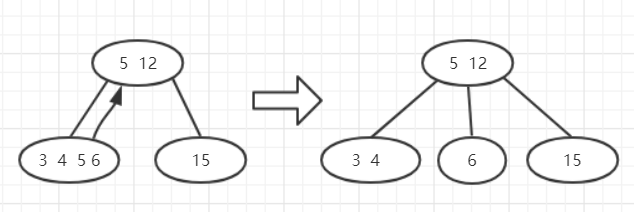
将5上升到父节点中,将原来的3456拆分为34和6连接到父节点
就像这样,当节点会有4个值的时候就提出第3个值向上传递并将原节点拆分,如果向上传递后父节点也有4个值了就再向上传递这就是2-3-4树的插入
2-3-4树的删除
删除同样伴随着对不满足2-3-4树的情况进行调整
如下: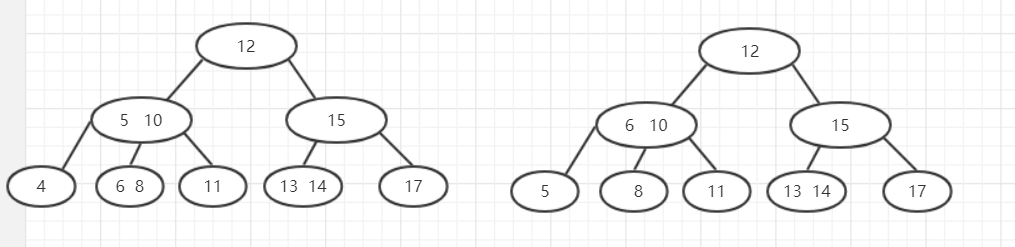
第一次删除4,当4没了的时候,不满足2-3-4树的性质,于是找其兄弟节点是否有可以弥补的,所以找到了6上移,将5移下来,保持了叶子节点深度不变
这次删除12,12是根节点,所以选择左子树最右边 代替他,11移走以后,就需要从父节点中把10移下来保持叶子结点的深度,同时把8和10合并。
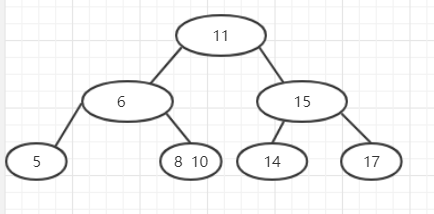
接下来删除了13,因为依然还是满足2-3-4树,所以不用调整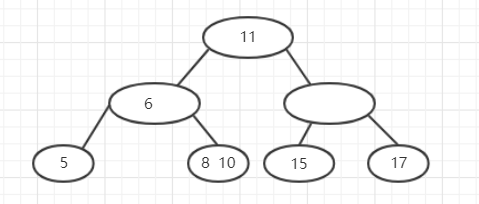
然后删除了14以后,为了保持叶子节点深度,继续从父节点那里向下移,于是15移到了下边,但是15的位置却空了,这个空位置还需要它的父节点来弥补,于是将11移到下面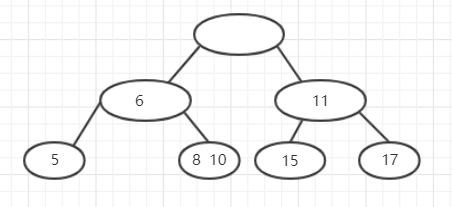
此时15和17的位置显然是不对的,所以将两个节点合并到11的右边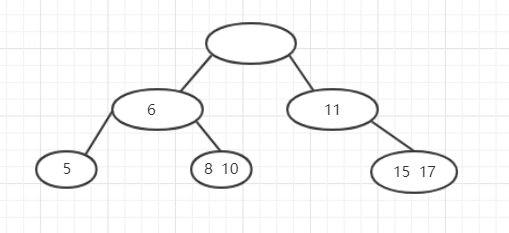
然后再将6和11合并为新的根节点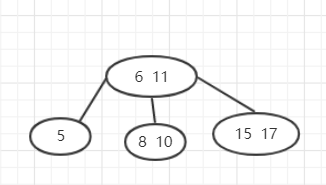
总结
对于2-3-4树的删除与插入,都是以保持叶子节点的深度相同为基础的。
插入的时候,就像是保持最下边一层为基础,向上填充,向上搭金字塔
删除的时候不断的用上边的节点来弥补下边的节点,保持地基的稳定,再缩减高度
但是我们也同样可以看出这些调整方式的复杂,所以2-3-4树实现起来不是很容易的