一.递归函数的弊端
递归函数虽然编写时用很少的代码完成了庞大的功能,但是它的弊端确实非常明显的,那就是时间与空间的消耗。
用一个斐波那契数列来举例
import time
#@lru_cache(20)
def fibonacci(n):
if n < 2:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
t1 = time.time()
print(fibonacci(35))
t2 = time.time()
print(t2 - t1) # 4.007285118103027
t1 = time.time()
print(fibonacci(36))
t2 = time.time()
print(t2 - t1) # 6.479698419570923
前面输入的数较小,所以算的还算很快,但输入到35、36来测试时已经要花上好几秒来计算了,而且36比35计算时间多了两秒多,可想而知数据再增大后消耗的时间增加的是越来越大的,因为这个递归函数的复杂性是O(2**n)
我们想一下这个函数递归的原理,流程,发现一个问题,计算fibonacci(35)的时候,是计算fibonacci(34)+fibonacci(33)的和,计算fibonacci(34)时,是计算的fibonacci(33)+fibonacci(32)的和,问题出现了,fibonacci(33)需要计算两次,那不是重复了嘛,我们继续递归向下拆分发现,几乎所有的递归函数拆分为两个函数的和时都会有重复计算,就想下面这个图:
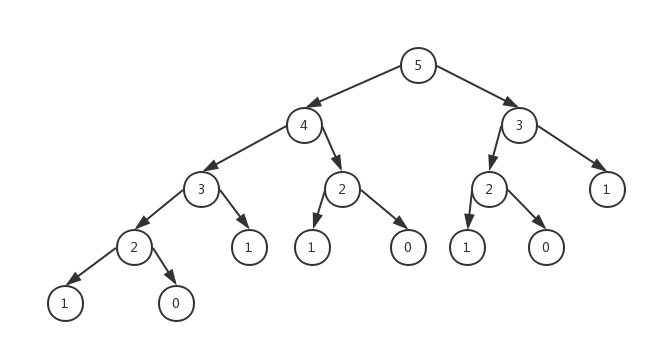
以fibonacci(5)举例,这个图里面有一大部分的数字是重复的,也就是说执行了很多的重复的函数,这使我们产生了一个想法,既然重复执行了,那我让它直接返回之前执行时的返回值不就行了,至于之前执行时的返回值,给他存起来不就好了吗,这就用到了我们下面要说的缓存思想
二.用缓存优化递归函数
我们定义一个装饰器来做函数的缓存
import time
def cache_decorator(func):
cache_dict = {}
def decorator(arg):
try:
return cache_dict[arg]
except KeyError:
return cache_dict.setdefault(arg, func(arg))
return decorator
@cache_decorator
def fibonacci(n):
if n < 2:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
t1 = time.time()
print(fibonacci(35))
t2 = time.time()
print(t2 - t1) # 0
t1 = time.time()
print(fibonacci(36))
t2 = time.time()
print(t2 - t1) # 0
当使用了缓存的方式后,发现计算所用的时间已经接近0,我们把数再改大一点
t1 = time.time()
print(fibonacci(300))
t2 = time.time()
print(t2 - t1) # 0.001026153564453125
t1 = time.time()
print(fibonacci(301))
t2 = time.time()
print(t2 - t1) # 0.0
这也太厉害了,当把数增大到300时,花费的时间才是0.001秒,而且t2的计算结果为0也证明了的确装饰器中缓存了数据,计算fibonacci(301)可直接从缓存中拿fibonacci(300)和fibonacci(299),我们用图来更清晰的解释
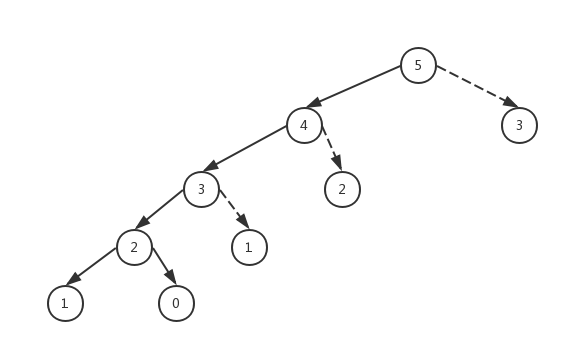
图中用虚线所指的结点都不需要重新计算了,只计算了不重复的数字,也就是意味着复杂度从O(2**n)降到了O(n)
这种缓存的思想,给我们的优化带来了巨大的收益
三.lru_cache装饰器
上面的装饰器是我们自己写的,但它不适用与其他函数,比如有多个参数的函数,但是python标准库为我们提供了一个非常方便的装饰器来进行缓存
它是functools模块中的lru_cache(maxsize,typed)
通过其名就能让我们了解它,它是通过lru算法来进行缓存内容的淘汰,
maxsize参数设置缓存内存占用上限,其值应当设为2的幂,值为None时表示没有上限
typed参数设置表示不同参数类型的调用是否分别缓存,这个参数的意思是如果设置为True,那么fibonacci(5)和fibonacci(5.0)将分别缓存,不存为一个。
lru_cache的使用只需要将上面我们自定义的装饰器替换为 lru_cache(None,False)即可。
参考《python高级编程(第2版)》