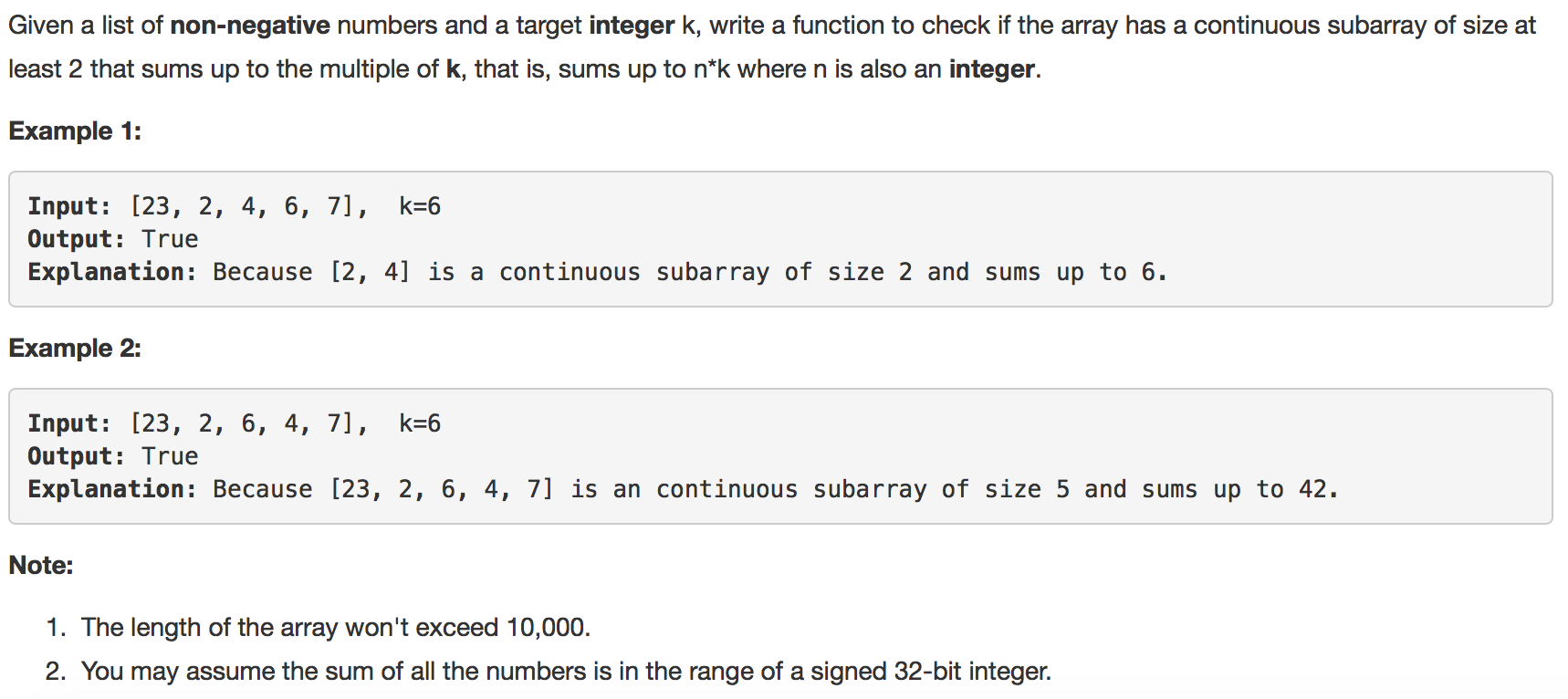
题目如下:
解题思路:本题需要用到这么一个数学定理。对于任意三个整数a,b,k(k !=0),如果 a%k = b%k,那么(a-b)%k = 0。利用这个定理,我们可以对数组从头开始进行求和,同时利用字典保存余数(key:余数,value:最早出现这个余数的元素下标),每累加一个元素都对k取余数,如果余数在字典中存在并且两个元素之间的下标差大于等于2,即表示存在这样的subarray。而对于k=0的情况,必须要出现至少两个出现至少连续两个0才能符合条件;当然,因为0*k = 0,所以如果数组中连续出现两个0,对任意的k都是满足条件的。
代码如下:
class Solution(object): def checkSubarraySum(self, nums, k): """ :type nums: List[int] :type k: int :rtype: bool """ continuousZero = False for i in xrange(len(nums) - 1): if nums[i] + nums[i + 1] == 0: continuousZero = True break if continuousZero == True: return True elif k == 0: return False dic = {} amount = 0 for i, v in enumerate(nums): amount += v reminder = amount % k if reminder == 0 and v != amount: return True if reminder in dic : if i - dic[reminder] >= 2: return True else : dic[reminder] = i return False