第二道绿题
这次大概真正懂了
看题面:
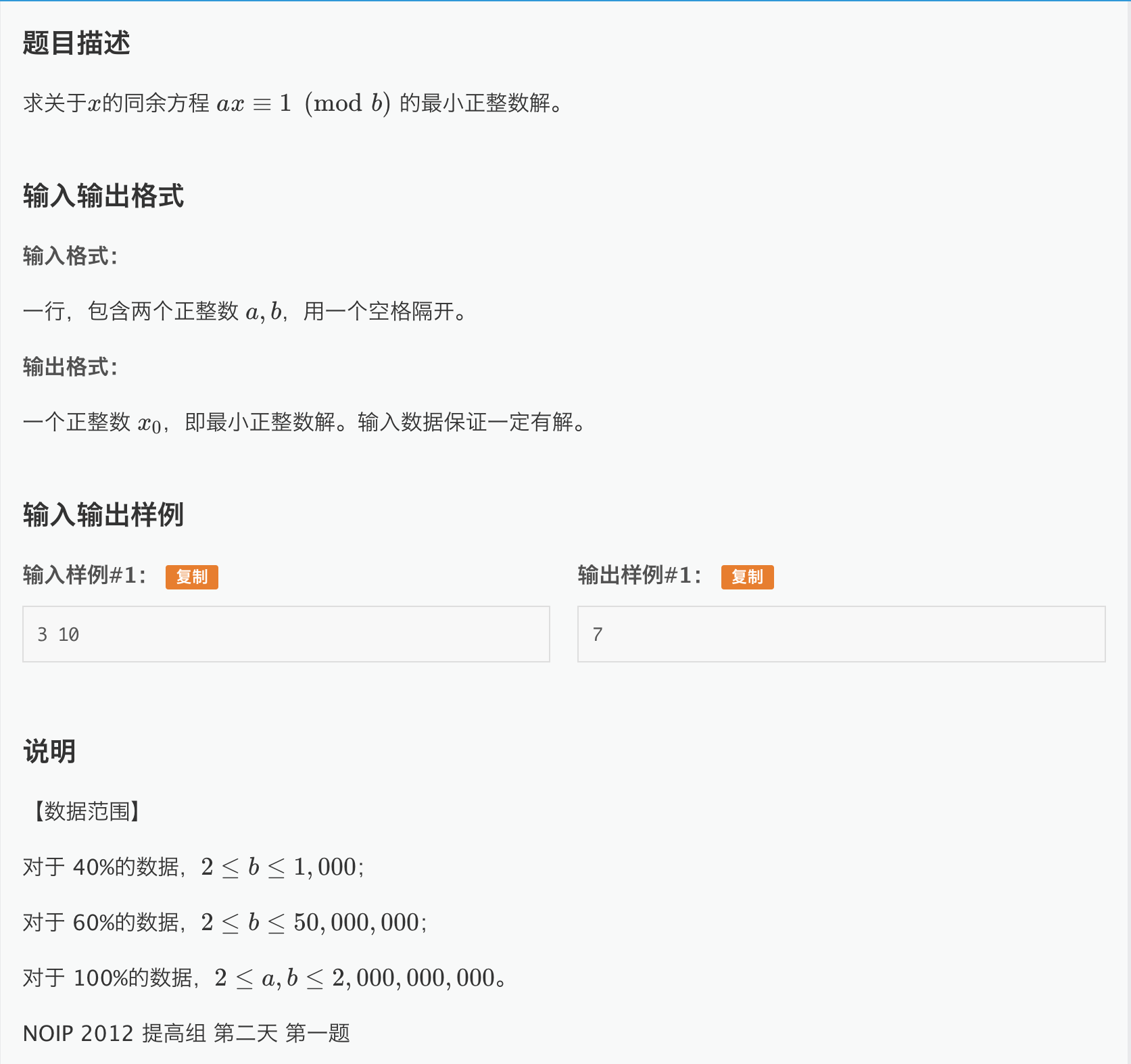
先了解一下公式 ax≡1(modb)
≡为恒等
这个公式翻译过来就是一个不定方程
ax+by=1
如果了解扩展欧几里得就知道这是一道exgcd的模版题//gg说的emmm
那我们先来了解一下gcd和扩展gcd吧(毕竟我本人当初也不会
gcd:
又称为辗转相除法
因为是求最大公约数,很好理解,就不再赘述了,上代码:
int gcd(a,b){ if (b==0) return a; else return gcd(b,a%b);//辗转相除 }
exgcd:
基本思路:对于不全为 0 的非负整数 a,b,gcd(a,b)表示 a,b 的最大公约数,必然存在整数对 x,y ,使得 gcd(a,b)=ax+by
证明:
显然,b=0时,gcd(a,b)=a,x=1,y=0
当ab!=0时
根据gcd可知:gcd(a,b)=gcd(b,a%b)
我们可以设x,x',y,y' //这里我们把a,b想成未知数,x,y想成常数,虽然较于正常方程来说有点别扭,但是适应一下就很好理解了
这样:ax+by=gcd(a,b)
bx'+(a%b)y'=gcd(b,a%b)
可得ax+by=bx'+(a%b)y'
我们知道a%b=a-(a/b)*b //这里的式子都是编程里用到的
则ax+by=bx'+ay'-(a/b)*by'
ax+by=ay'+b(x'-(a/b)y')
这样就可以发现取等的条件了:x=y'&&y=x'-(a/b)y'
如此,求x',y',我们可以设x'',y''
x'=y''&&y'=x''-(a/b)y''
如此一直推下去,我们可以用递归来解决
int exgcd(int a,int b,int &x,int &y) { if(b==0) { x=1; y=0; return a; } int r=exgcd(b,a%b,x,y); int t=x; x=y; y=t-a/b*y; return r; }
这里的b总会推成0,递归就结束了
我们现在已经了解了exgcd
现在再看这道题ax+by=1,求x的最小整数解
方程 ax+by=1有解的必要条件是 1%gcd(a,b)=0
那么相应的a,b互质
我们只需要求出ax+by=gcd(a,b)中x的最小整数解就可以了
显然,这就是一道exgcd的板子题 //然而您需要推出来上面的式子才能发现(。ì _ í。)
等等 可是题目要求的是x为正整数
我们用exgcd求出的x不一定是最小正整数
所以我们要将x+或-b直到x恰好大于0
然后您就切了这道题了!(tql!
#include<cstdio> #include<iostream> typedef long long ll;//为了避免数太大而开了long long,事实证明其实不需要…… using namespace std; ll x,y; void exgcd(ll a,ll b) { if(b==0) { x=1; y=0; return ; } exgcd(b,a%b); ll k=x; x=y; y=k-a/b*y; }//exgcd int main() { ll a,b; scanf("%lld%lld",&a,&b); exgcd(a,b); while(x<0) x+=b; x%=b;//使x为最小整数解 printf("%lld",x); return 0; }
//本苣蒻第二篇题解祭
//真正理解的第一道绿题祭
//谢谢洛谷题解orz