(gg直接讲的用矩阵求斐波那契数列
(原地死亡
(全程一脸懵逼
(然后看了半个点题解
首先,什么是矩阵呢
就是类似于这样的东西(里面可以填什么复数啊,实数啊的
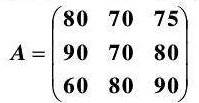
然后矩阵的基本运算了解一下
加法很简单emmmm(不说了
乘法需要了解一下,毕竟比较神奇
(A * B != B * A 难道不觉得违背常识吗?多神奇啊!
(我觉得讲矩阵乘法讲的最好,最通俗易懂的是曹天元所著的《上帝掷骰子吗》中 chapter 05 part 3,推荐看一下
矩阵乘法嘛。。。只要知道基本要求就那么求就行了emmmm
两个矩阵,第一个矩阵的列数与第二个矩阵的行数相等时即可相乘
举个栗子

然后正经的解释和公式是酱的:
设A为 m * p 的矩阵,B为 p * n 的矩阵,那么称 m * n 的矩阵C为矩阵A与B的乘积,记作 C = AB
其中矩阵C中的第 i 行第 j 列元素可以表示为
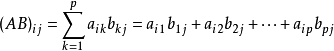
需要注意的是
(来源百度百科【特别鸣谢orz
大概理解了矩阵乘法之后我们来看看这道题吧
标签是矩阵乘法诶那怎么用呢【考场上能想到矩阵乘法的都tql!!!


一看数据范围,显然正常递推会只得60分
如果想要拿到满分需要想一下优化
然后我们刚刚说到矩阵
(我也不知道他们怎么想出来用矩阵的 tql!!!
我们会发现矩阵的定义里有这么一个东西叫做单位矩阵
主对角线上的元素都为1,其余元素全为0的n阶矩阵称为n阶单位矩阵
(主对角线就是左上角到右下角的那条对角线
它长这个样子
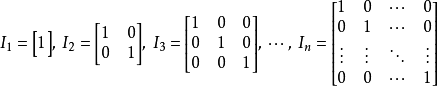
它有什么用呢?
所有矩阵乘上单位矩阵都等于本身
(哇看起来好鸡肋23333
(说实话我也不知道它有什么用
(但是它给我们提供了一个思路,如何模拟斐波那契数列
如果我们构造一个矩阵(符合斐波那契数列的规律
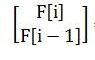
我们要推出它从何而来
因为我们知道 F [i] = F [i - 1] + F [i - 2]
那么某两个矩阵相乘能够得到这样一个矩阵
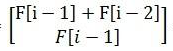
因为我们要找规律嘛,所以其中一个矩阵一定与构造的那个矩阵性质相似
即为
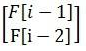
那再逆着推出来另一个矩阵就很简单了
最后得到
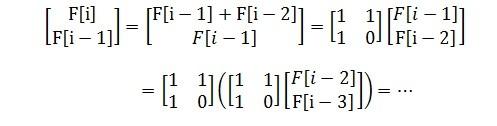
这样一直推下去
一定会推到 i = 2 ,i - 1 = 1
这样的话定义一个初始矩阵两行全为一,再反复乘这个固定的
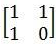 矩阵
矩阵
就能得到最终的结果
因为最初的 F [1],F [2]已经定义了
所以要求出F [n]的值,我们只需要乘上固定矩阵的 n - 2次方即可
这里需要用到矩阵快速幂
其实和快速幂没什么区别,只是需要写一个矩阵相乘的函数或是重置运算符
但是一定要记住,因为矩阵相乘 A * B != B * A
所以如果初始矩阵与固定矩阵乘反了的话,结果就不一样了
如果反过来,初始矩阵就应该是一行两列的矩阵了
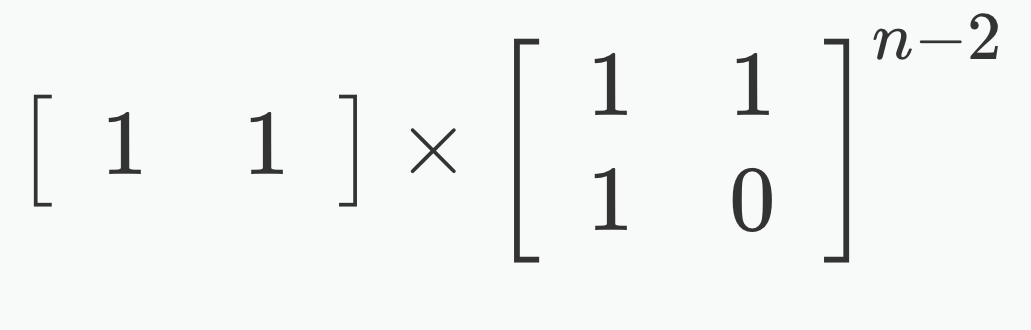
(我就是这样写的23333
最后的结果就是第一行第一列的数了
看代码吧~
#include<cstdio> #include<cstring> #define ll long long #define mod 1000000007//别忘了膜 using namespace std; struct matrix { ll a[3][3]; matrix() { memset(a,0,sizeof(a)); } } ans,base;//用结构体存放矩阵,并在结构体中将数组一次性初始化 matrix operator * (const matrix &x,const matrix &y) { matrix z; for(ll i = 1; i <= 2; i++) for(ll j = 1; j <= 2; j++) for(ll k = 1; k <= 2; k++) z.a[i][j] = (z.a[i][j] + x.a[i][k] * y.a[k][j] % mod) % mod; return z; }//重置运算符,不然写个函数也行 void quickpow(ll b) { while(b) { if(b & 1) ans = ans * base;//别乘反了 base = base * base; b >>= 1; } }//快速幂 int main() { ll n; scanf("%lld",&n); if(n <= 2) { printf("1"); return 0; } base.a[1][1] = base.a[1][2] = base.a[2][1] = 1;//固定矩阵 ans.a[1][1] = ans.a[1][2] = 1;//初始矩阵 quickpow(n - 2); printf("%lld",ans.a[1][1] % mod); return 0; }
emmmmm
那么这道题就讲完啦
第二道蓝题祭~