转自:http://www.zbrushcn.com/jichu/zbrush-cy-3dsys.html
Polygon(多边形)

多边形是一种形状,通过在3D空间连接几个点而创建,最简单的形式就是三角形,连接3个点而形成,少于3个点,就只是两个连接的点(这种连接称之为边缘)。
PolyMesh(多边形网格)

多边形网格是3D空间里的某个物体,由若干连接的多边形形成,多边形组合组成网格(也就是Poly-Mesh),在ZBrush里,网格可以由四角形或三角形的多边形组成。
3D Primitives(3D基本体)
3D基本体是3D里最基本的形状和构建模块,比如立方体、圆锥体、球体、圆环体、圆柱体等,它们看起来很像相同形状的其他多边形网格,它们都有边缘连接点,都能创建多边形网格。但是,3D基本体是一种依靠数学数据定义自身形状的物体,这意味着你可以在将基本体转换为多边形网格之前大改特改该基本体,ZBrush提供了很多更加高级的基本体,比如Gear3D。

如上面的图片,可以将左边的环形物变成右边“急速旋转的状态”,无需任何建模,只需调整数学数据(超级简单,使用初始调色板中的滑动条即可)。
Geometry resolution(几何分辨率)
几何分辨率的另一个叫法是多边形密度,它和模型的多边形数量有关,一个简单的立方体属于“低分辨率”一类,因为它仅有6个多边形形成网格。如果细分立方体,ZBrush(及大多数3D软件)会将每个多边形拆分成4个多边形。如果再继续细分立方体网格,多边形的数量将呈指数增加(提高分辨率),形成“高分辨率”模型。
“低分辨率”立方体VS“高分辨率”立方体(低分辨率立方体被细分了4倍):

Subdivision level(细分级别)

细分级别和物体的分辨率直接相关,基本上每细分一次物体(每个多边形会拆分为4个),ZBrush便会创建新的细分级别,这一点很好,因为这样就可以在同一个模型的不同分辨率级别之间来回移动。
Topology(拓扑)

你可能经常碰到这个单词,我喜欢这样理解拓扑:拓扑是为实现某个特定目的,将3D多边形排列成模型的科学和实践,就好像为你的3D模型创建贴图一样。
例如,你需要一个栩栩如生的模型拓扑,那么多边形则需要以特定的方式进行排列,移动的时候不会被损坏或者将整体形状变形。
Edge(边)

边即连接空间里两个点的一条线,是多边形最简单的形式,三角形通常有3条边。
边可以由两个多边形共享,当你的模型的所有边由2个多边形共享,就会用到术语“Closed geometry”,某些情况下,边不被2个多边形共享,这种的被称为“Open geometry”。
Points(点)
点应该是3D艺术里最基本的概念了,它是3D空间里带有X、Y、Z信息的一个坐标。
Face(面)

在3D里,面通常指的是模型的平面区域,例如,立方体由8个点、12条边和6个面组成,每个多边形(由3或4个连接的点形成)就是一个面。
Normals(法线)
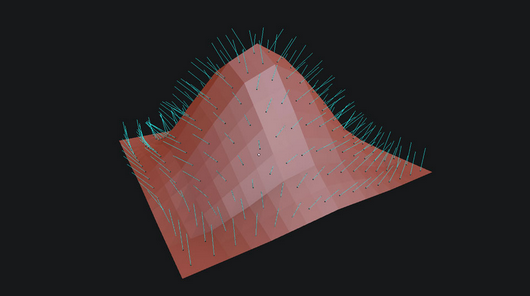
在3D艺术里,法线是一种矢量或直线,垂直于它的下垫面(通常指的是物体的表面),法线由3D软件用来定义与灯光的交互,特别是在使用着色器时。
Symmetry and mirror(对称和镜像)

一般来说,这两个概念的含义是一样的:保持两边相同(例如+x和-x),在ZBrush里,使用对称和镜像选项有很多种好方法,区别就是在对称状态下,雕刻的时候可以看见两边的变化,而选择镜像时,是先处理模型的一边,这一边完成之后再镜像另一边。
Polyframe/Wireframe(多边形框/线框图)

在3D软件里,Wireframe也是经常会用到的,这个术语在ZBrush里叫做Polyframe,两者基本上是一样的,指的是物体上连接所有点而创建的看得见的“网格”,你可能见过一些wireframe渲染,能够很好地展示多边形密度或者模型的拓扑结构。
Displacement map(置换贴图)
置换贴图是一种灰度图像,也称为高度图,用来将凹凸贴图或法线贴图渲染为真实的几何体,不同于法线贴图或凹凸贴图,置换贴图可以真正“置换”表面,图像的白色区域将几何体“拉出来”,黑色区域将几何体“推进去”。

高度图和置换贴图意思差不多,但更常用在地形建模环境里。
UV map(UV贴图)
UV贴图主要用来控制2D纹理在3D物体周围包裹的方式,同样的,X、Y、Z指的是3D空间里的坐标,U和V是定义2D空间里的坐标的字母。

UV贴图的目的是找到一种最有效的方式,将3D物体的所有多边形布局到2D平面图像中。
Bump map(凹凸贴图)

凹凸贴图也包括灰度图像,常用于在渲染3D对象时模拟裂缝、皱纹、毛孔和小的细节, 凹凸贴图模拟表面位移,使用多边形的表面法线创建相对于相机视角的像素高度,换句话说,它存储灰度值“强度”,相当于更简单的置换贴图,在渲染的时候假装位移物体表面。
Normal map(法线贴图)

法线贴图非常类似于凹凸贴图,都用来实现相同的目的。但法线贴图更准确更强大,因为它不仅存储“强度”,还通过使用RGB值存储法线的方向,与凹凸贴图截然相反的是,法线贴图可以模拟向任何方向移动的像素。
Alpha(通道)
通常来说“Alpha”指的是透明度或者3D里的遮罩,但在ZBrush中,Alpha是一种超级灰度图像(你也可以说它是一种更精确的凹凸贴图),因为ZBrush可以生成16位alphas。在ZBrush里可以以多种方式使用Alpha,例如可以通过简单地修改笔刷alpha而完全改变笔刷的形状,当然还可以通过创建交互式置换几何结构的非常微小的细节来调整模型的几何结构。
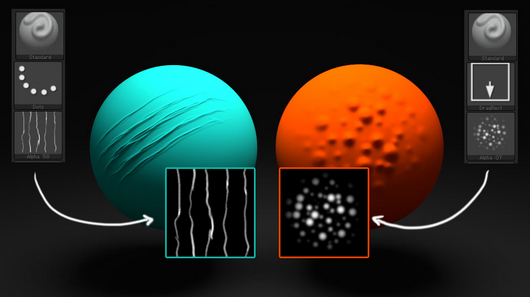
Alphas大多在雕刻过程结束的时候使用,用来添加非常小的细节。
MatCap(材质捕捉)

MatCap即“材质捕捉”。MatCaps是ZBrush使用的材质,包括环境属性,如灯光和反射光,可以画一个你想要的球体,然后将它作为你的MatCap图像。
Stroke(笔触)

笔触是一种与笔刷关联的功能,它可以决定笔刷如何应用到模型表面上。
Tris(三角形)

三角形是多边形最简单的形式,由三点一面组成。
Quads(四边形)

四边形多边形形成一个平面,由4点、4边和一个单独的面组成。
Zsphere(Z球)

Zspheres是ZBrush中的一个独特的高级工具,可以快速创建大枢,然后再转变为模型,还可以使用它们在3D里画草图,“操纵”自己的模型来给它们摆姿势。
PolyGroups(多边形分组)

这是一种非常直接却很强大的概念,Polygroups可以让你在3D物体内部创建分组,加快你的工作流程,帮助你创建非常酷的效果,你还可以使用Polygroups轻松选择和隐藏模型的某些部分。
AO(环境光遮蔽)

AO全称Ambient Occlusion(环境光遮蔽),用来模拟网格之间的接触阴影(通常是非常柔和的阴影),AO在贴图形式和合成渲染过程里很常见(就像纹理贴图)。
SSS(次表面散射)

SSS即Sub-Surface Scattering(次表面散射),指的是灯光与半透明材料交互产生的效果。
Antialiasing(抗锯齿)
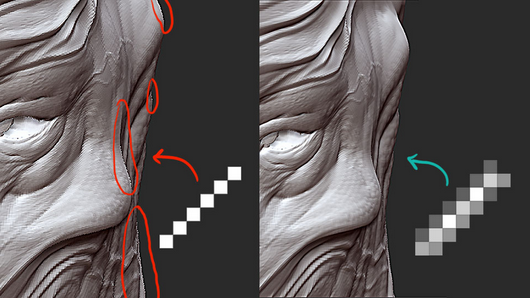
Antialiasing,一种技术,或者说是消除锯齿边缘的过程(也称为“阶梯效应 ”)。处理像素的时候,创建垂直或水平直线很容易,问题是创建对角线就难了,每一个像素都是一个正方形,所以对角对齐的时候,正方形在拐角处想接,而不是并排的,抗锯齿过程可以评估像素之间丢失的数据,采集周围的像素,以创建更加柔和的过渡,让对角线看起来更加平滑。
Dynamesh(动态网格)
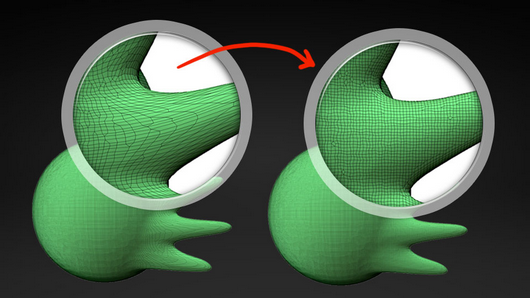
Dynamesh可以说是改良模型的一种功能,也是在ZBrush里实现构建体积的一种好方法,它可能最接近于使用真正的粘土,因为你不必担心拓扑结构或者连续性。
有了Dynamesh,你可以拉、推或者分离模型,ZBrush会动态生成匹配物体形状的必要多边形,同时保持均匀分布。
SubTool(子工具)
Subtools不是图层,它是模型上的单独对象,在每个Tool里以列表的形式呈现。
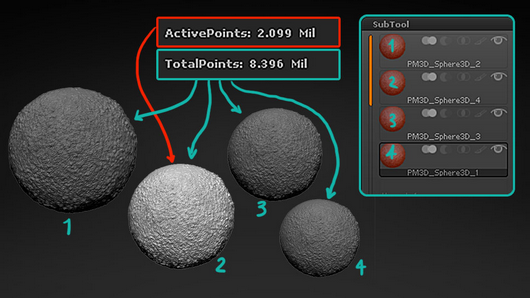
在多个SubTools的帮助下,便可以获得有着成千上万多边形的超细模型,即便你的系统只能处理100万个多边形,你也可以获得2000万多边形模型,由20个SubTools组成,每个SubTool有100万个多边形。