法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说:在世界中心贝拿勒斯(在印度北部)的圣庙里,一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候,在其中一根针上从下到上地穿好了由大到小的64片金片,这就是所谓的汉诺塔。不论白天黑夜,总有一个僧侣在按照下面的法则移动这些金片:一次只移动一片,不管在哪根针上,小片必须在大片上面。僧侣们预言,当所有的金片都从梵天穿好的那根针上移到另外一根针上时,世界就将在一声霹雳中消灭,而梵塔、庙宇和众生也都将同归于尽。

这个题目是大二学数据结构中的递归时的经典题目。这个题目是对递归思想最典型的体现。我们现在用python来实现它。
假设有N个圆盘(从大到小),三个柱子,O,M,T。开始N个盘子按从大到小的顺序套在柱子O上,要按照汉诺塔的规则,将这N个圆盘转移到T柱上,M柱可以作为中转。
我们以递归的思想来分析这个问题。
我们把圆盘从小到大编号为1,2,......N。
1、如果N=1,只有一个盘子的话,直接将圆盘从 O 移到 T即可。
2,如果N=2,先将1号盘移动到M,再将2号盘从O移动到T,再将1号盘从M移动到T。
3,如果N>=3呢?这里就用到递归思想了
(1)我们先将上面的N-1个盘子从O移动到M
(2)将N号盘子从O移动到T
(3)将N-1个盘子从M移动到T
那我们用python来实现它。
我们定义方法 move( n, o, m, t )。函数的功能就是将 n个盘子,从柱子o移动到t,m作为中转站。
def move( n, o, m, t ):
if n == 1:
print("move pan " + str(n) + " from #" + str(o) + " to #" + str(t) ) #move pan 1 from #1 to #2
else:
move(n-1, o, t, m)
print("move " + str(n) + " from " + str(o) + " to " + str(t) )
move(n-1, m, o, t)
我们来执行它:
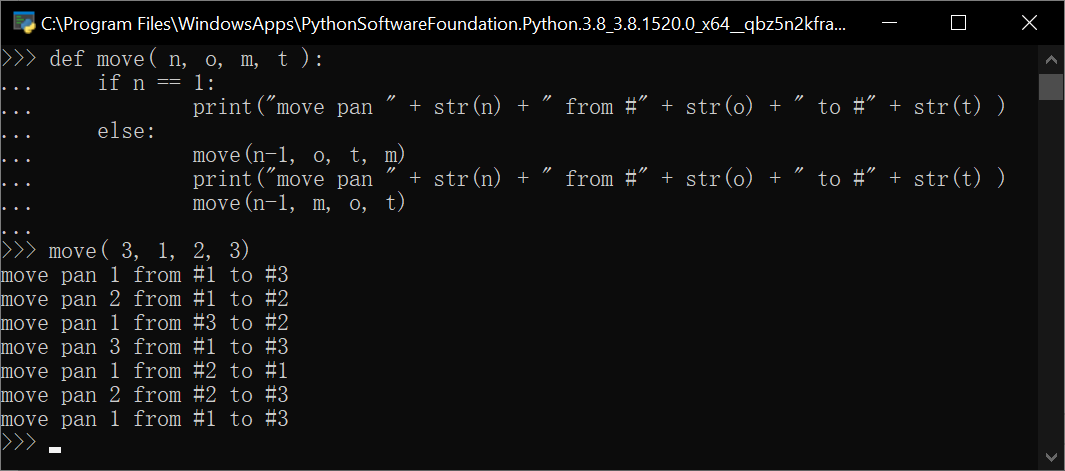
move( 3,1,2,3 )
结果:
move pan 1 from #1 to #3
move pan 2 from #1 to #2
move pan 1 from #3 to #2
move pan 3 from #1 to #3
move pan 1 from #2 to #1
move pan 2 from #2 to #3
move pan 1 from #1 to #3