【2020.11.30提高组模拟】柱形图(histogram) 题解
题意简述
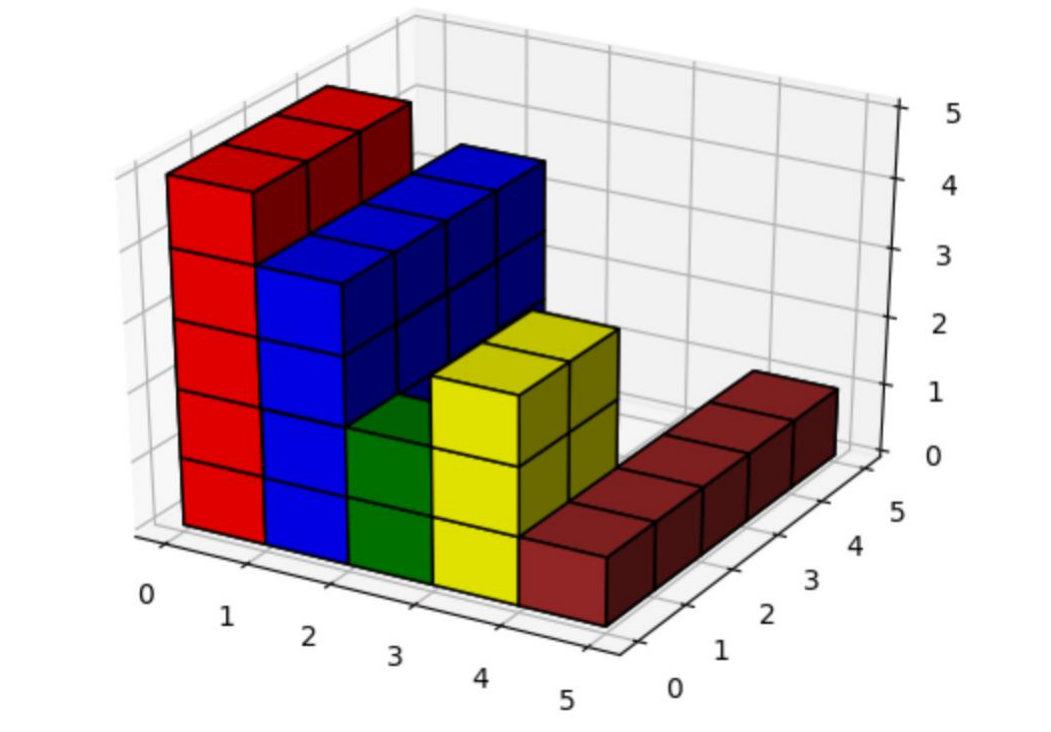
有(n)个长方体并排这样放着,每种颜色的长方体的宽度都为(1),高(a_i)长(b_i)。
求在这些长方体内部最大能够放入的长方体的体积。
(nle200000).
Solution
这个问题可以在(O(nlog^2n))的时间复杂度内解决。
设(f(i,j)=min(a_i,dots,a_j),g(i,j)=min(b_i,dots,b_j))。
这个问题就被转化成了找到一个区间([i,j])使得(max f(i,j)cdot g(i,j)cdot (j-i+1))。
考虑分治((divide-and-conquer))。
(solve(lo,hi))将找到区间([lo,hi])中横跨区间(mid)的最优的区间。他将递归调用(solve(lo,mid-1))和(solve(mid+1,hi))。
为了递归合并区间,我们设([l,r])是一个(lin[lo,mid],rin[mid,hi])的区间。我们考虑四种情况:
- (f(l,r))和(g(l,r))都是由左半部分决定,即(f(l,r)=f(l,mid),g(l,r)=g(l,mid)).
- (f(l,r))和(g(l,r))都取决于右半边,即(f(l,r)=f(mid,r),g(l,r)=g(mid,r)).
- (f(l,r))取决于左侧,(g(l,r))取决于右侧.
- (f(l,r))取决于右侧,(g(l,r))取决于左侧.
情况(1/2)是类似的,情况(3/4)是类似的,所以我们只需要考虑情况(1/3)。
情况(1)
(f(l,r))和(g(l,r))都是由左半部分决定
注意到这意味着(f(l,mid)le f(mid,r),g(l,mid)le g(mid,r)).
我们可以使用双指针法在(O(hi-lo))的时间内解出来,所以总时间复杂度就变成了(O(nlog n)).
情况(3)
(f(l,r))取决于左侧,(g(l,r))取决于右侧
注意到这意味着(f(l,mid)le f(mid,r),g(l,mid)le g(mid,r)).
这个就没有情况(1/2)那样可以在(O(nlog n))内解出来。
它存在(O(nlog^2n))的解法,我们将首先介绍一种(O(nlog^3n))的解法。
其中(langle(a,b),(c,d) angle)表示向量((a,b))和((c,d))的点积。
注意到第一个向量仅仅依赖于(l),第二个向量仅仅依赖于(r).
对于一个固定的(l),我们希望找到一个(rin[a(l),b(l)])使得这两个向量的点积最大。如果(r)不属于那个区间, 我们可以计算第二个点集的凸包,然后用三分查找找到对于每个(l)的最优的(r)。但是现在,我们可以对这些点按照它们的横坐标排序,然后建一棵线段树,这棵线段树的每个节点都记录着相应的凸包。所以对于每个(l)我们将会查看线段树上的(O(log n))个节点,然后以单次 的时间在每个节点对应的凸包内做三分查找。 这给我们带来了一个(O(nlog^3n))的算法,因为我们需要再用一个分治统计答案。
现在我们想要摆脱二分,注意到点(f(l,mid)cdot (-l+1,1))随着(l)增加而向逆时针移动,所以凸包上的极值点 也会向逆时针移动,对于线段树上的每个节点,我们可以在(O(n))的时间内完成一次询问,通多记录上次询问的极值点的指针的方式。这给我们带来了一个(O(nlog^2n))的方法。