【2020.11.30提高组模拟】剪辣椒(chilli) 题解
题意简述
给你一棵树,删去两条边,使得形成的三棵新树的大小极差最小化。求最小极差.
(3le nle 200,000).
Solution
假设根为(1).
设删去的点意为这个点到其父亲的连边被删了,关系指一个点是另一个点的祖先,(size_x)为以(x)为根的子树大小,(a,b,c)是三棵新子树的大小。
答案即为
那么只会有两种情况:
被删去的点有关系
不妨设(x)是(y)的祖先
被删去的点无关系
显然这里就有一种比较暴力的方法了,时间复杂度(O(n^2))。
考虑优化。
optimization
在(dfs)中,我们维护两个(set:A,B)
当进入点(x)时,把(size_x)放入(A)中;
当走出点(x)时,把(size_x)从(A)中删除并放入(B)中;
这样(A)里的元素就是(x)的直接祖先,(B)中是与(x)无关系的点(不需要考虑到还没有访问到的点,因为反过来会遍历到的)
接下来每到一个点(x),我们继续考虑两种情况:
被删去的点有关系
假如我们要删去点(x),另一个被删去的点为y应使得(n-size_y)和(size_y-size_x)这两个子树的大小最平均,即(n-size_y=size_y-size_xRightarrow 2size_y=n+size_x)。
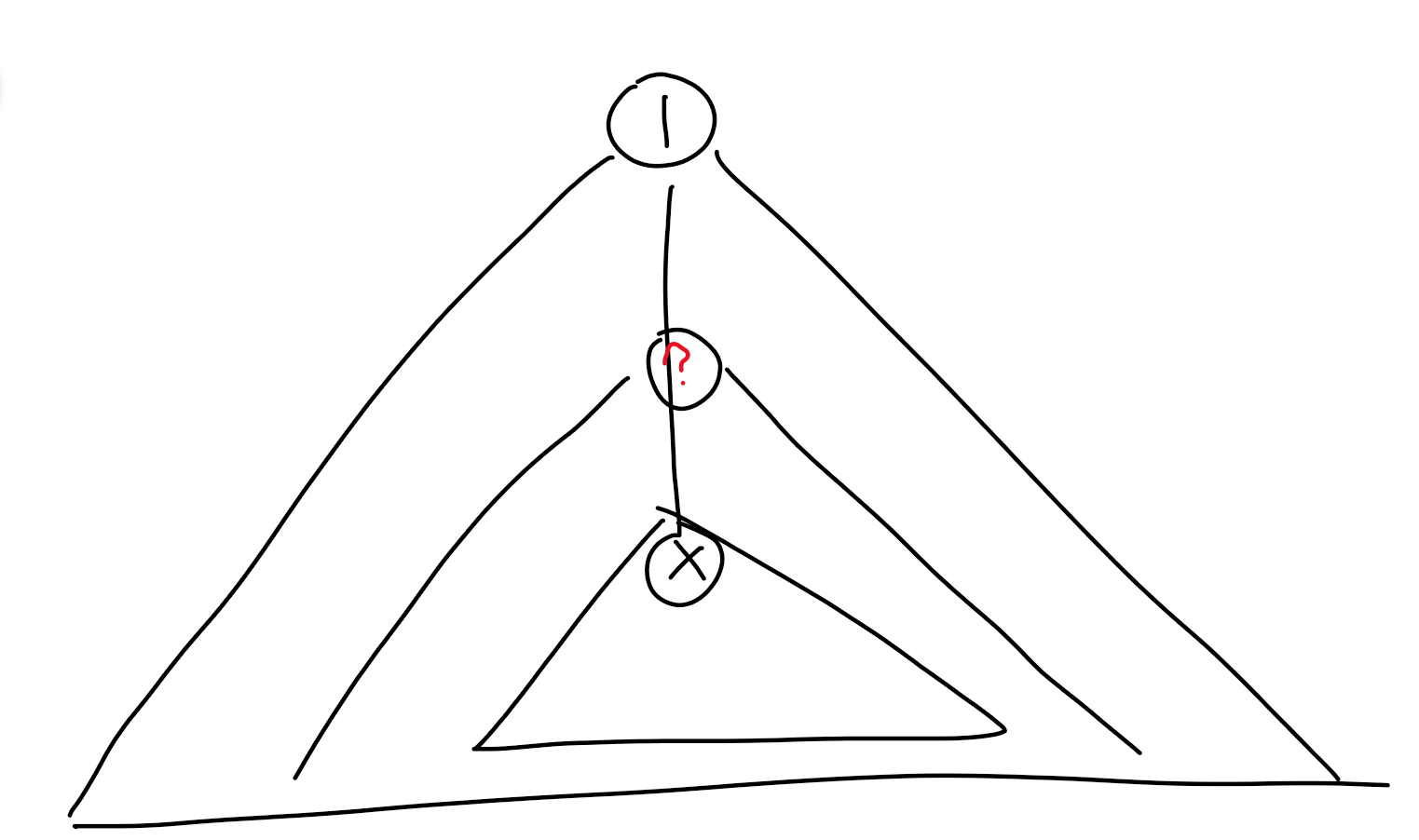
我承认我图很丑,我谢罪……
那么我们就去(A)中找一个值接近上面(size_y)的值并更新答案。
当然,不一定会有正好相等的,应该用lower_bound()后在让指针iter--,进行两次判断。
被删去的点无关系
同理假如我们要删去点(x)和与它无关系的点(y),就要使得(size_y)和(n-size_x-size_y)这两个值最相近,即(size_y=n-size_x-size_yRightarrow 2size_y=n-size_x)。
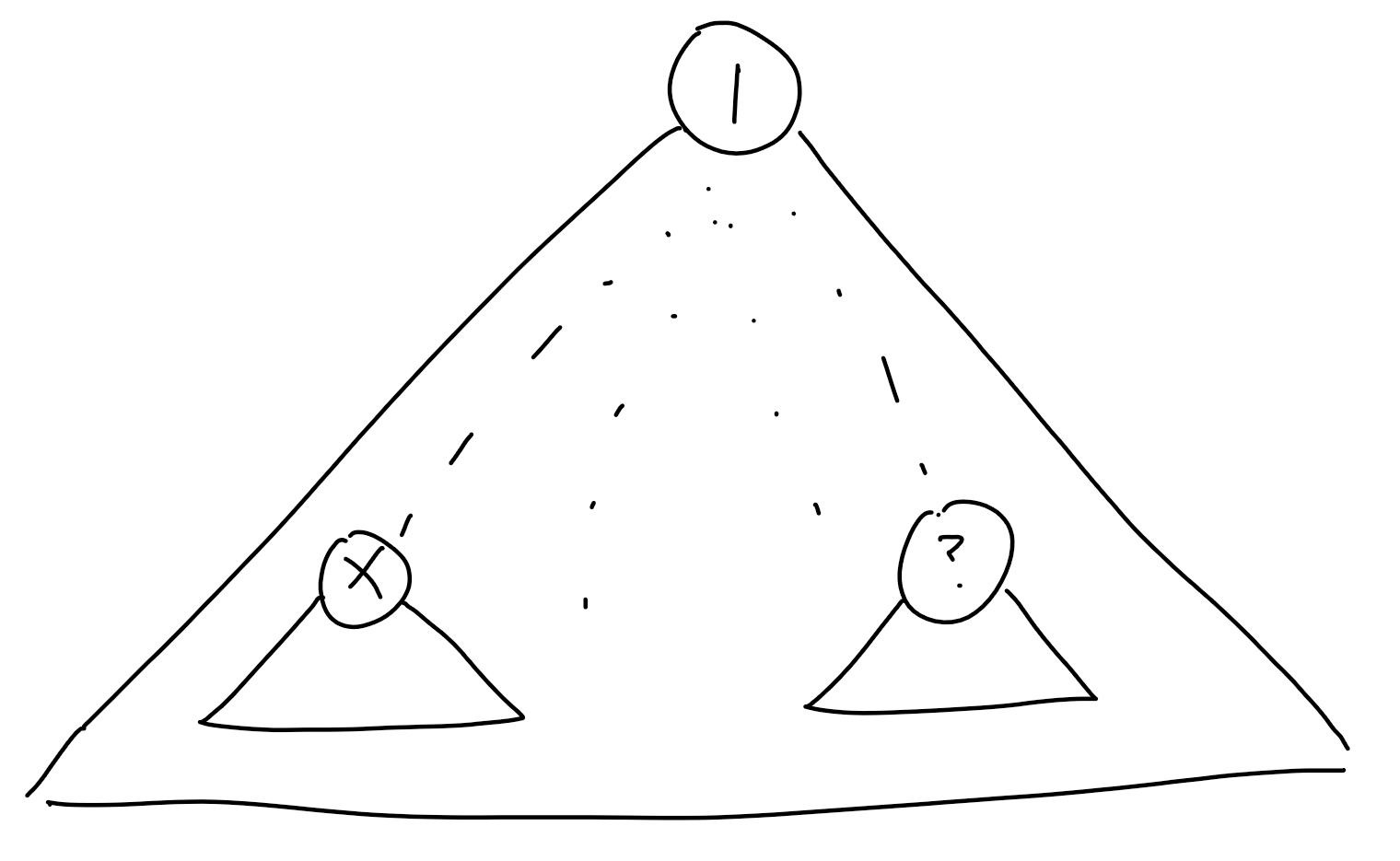
我承认我图很丑,我再次谢罪……
那么我们就去(B)中找一个值接近上面(size_y)的值并更新答案。
Code
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<map>
#include<set>
#include<queue>
#include<vector>
#define IL inline
#define re register
#define LL long long
#define ULL unsigned long long
#ifdef TH
#define debug printf("Now is %d
",__LINE__);
#else
#define debug
#endif
using namespace std;
template<class T>inline void read(T&x)
{
char ch=getchar();
int fu;
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
x*=fu;
}
inline int read()
{
int x=0,fu=1;
char ch=getchar();
while(!isdigit(ch)&&ch!='-') ch=getchar();
if(ch=='-') fu=-1,ch=getchar();
x=ch-'0';ch=getchar();
while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();}
return x*fu;
}
int G[55];
template<class T>inline void write(T x)
{
int g=0;
if(x<0) x=-x,putchar('-');
do{G[++g]=x%10;x/=10;}while(x);
for(int i=g;i>=1;--i)putchar('0'+G[i]);putchar('
');
}
int n;
int ans=100000000;
set<int>A,B;
int sze[200010];
int head[400010],ver[400010],nxt[400010];
int cnt;
void insert(int x,int y)
{
nxt[++cnt]=head[x];
ver[cnt]=y;
head[x]=cnt;
nxt[++cnt]=head[y];
ver[cnt]=x;
head[y]=cnt;
}
void dfs1(int x,int fa)
{
sze[x]=1;
for(int i=head[x];i;i=nxt[i])
{
if(ver[i]!=fa)
{
dfs1(ver[i],x);
sze[x]+=sze[ver[i]];
}
}
}
IL void upd(int x,int y,int z)
{
ans=min(ans,max({x,y,z})-min({x,y,z}));
}
void dfs2(int x,int fa)
{
// cout<<sze[x]<<endl;
A.insert(sze[x]);
set<int>::iterator iter;
iter=A.upper_bound((sze[x]+n)/2);
if(iter!=A.end())
{
upd(sze[x],*iter-sze[x],n-*iter);
}
if(iter!=A.begin())
{
iter--;
upd(sze[x],*iter-sze[x],n-*iter);
}
iter=B.upper_bound((n-sze[x])/2);
if(iter!=B.end())
{
upd(sze[x],*iter,n-sze[x]-*iter);
}
if(iter!=B.begin())
{
iter--;
upd(sze[x],*iter,n-sze[x]-*iter);
}
for(int i=head[x];i;i=nxt[i])
{
if(ver[i]!=fa)
{
dfs2(ver[i],x);
}
}
A.erase(sze[x]);
B.insert(sze[x]);
}
int main()
{
// freopen("chilli.in","r",stdin);
// freopen("chilli.out","w",stdout);
n=read();
for(int i=1;i<n;i++) insert(read(),read());
dfs1(1,0);
dfs2(1,0);
cout<<ans;
return 0;
}
End
一次性写完代码运行一下,没仔细看就以为自己WA了就来写Solution。写完Solution准备来Debug,写完的Debug语句再运行发现代码是对的!Woc泪目!
绝了,(std)是老外写的吧,全是c++11,auto啥的
所以我也用了初始化列表+max(lists)
嘿嘿,还挺方便的呢
我在跑操的时候突然发现,这道题有些平衡树的思想。(而不是把(set)当成离散化bool数组来用)
不断的插入值,删除值,求前驱后继……不就是平衡树嘛?
看来我需要加强模型转化能力。