二叉堆

一、定义

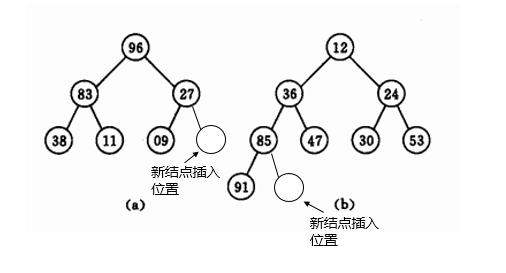
二叉堆是堆的一种，使用完全二叉树来实现。所谓完全二叉树，即高度为n的二叉树，其前n-1层必须被填满，第n层也要从左到右顺序填满。在二叉堆中，所有非终端结点的值均不大于（或不小于）其左右孩子的值。若非终端结点的值均不大于其左右孩子结点的值，这样的二叉堆叫做小根堆（下图中（b）），小根堆根结点的值是该堆中所有结点的最小值；同样的，当所有非终端结点的值都不小于其左右孩子的值时，这样的对叫做大根堆（下图中（a）），大根堆根结点的值为改堆所有结点的最大值。利用堆的此性质，可以实现堆排序。

说明：小根堆和大根堆的实现没有太大的区别，所以下面以小根堆为例。

二、二叉堆的操作

堆一般使用数组来构建，假设为数组a[]，结点通常存储在a[1]，这样对于下标为k的结点a[k]来说，其左孩子的下标为2*k，右孩子的下标为2*k+1。

1、插入结点到堆中.

由于小根堆是由数组实现的完全二叉树，所以插入的位置应该是完全二叉树的最后一个位置（如下图所示），对于小根堆来讲，需要满足两个性质：（1）堆为完全二叉树；（2）堆中每个结点的值都不大于其左右结点的值。插入结点可能会破坏这两条性质，所以在插入结点后需要对堆进行调整。调整方法为：将插入的结点与其父结点比较，若小于其父结点的值，则交换两者。重复此操作，直至该结点不比其父结点小，或者该结点成为根结点。可以通过插入结点到一个已经存在的堆中，也可以通过不断插入结点来构建一个堆。

 

2、删除堆顶元素（堆排序）

删除堆顶元素（根结点）后，会得到左右两棵子树，此时将堆中最后一个元素移到堆顶，然后自上而下调整，将该结点与左右孩子结点比较，此时会有三种情况：

（1）结点的左右孩子均为空，此时调整结束；

（2）结点只有左孩子，此时将该结点与其左孩子比较。若结点大于其左孩子，则两者交换，否则调整结束；

（3）结点左右孩子都非空，则将该结点与左右孩子之间的较小者比较，若小于则交换，否则调整结束；

重复此过程，直到该结点不大于其左右孩子结点，或者该结点为叶子结点。

3、实现代码

#include <algorithm>
#include <iostream>
using namespace std;

class MinHeap
{
private:
    int* heap;        //存储堆
    int cur;          //堆中结点个数

    /*插入结点后，向上调整*/
    void adjustUp();    

    /*删除结点后，向下调整*/
    void adjustDown(int idx);
public:
    MinHeap();
    ~MinHeap();

    /*插入值为val的结点*/
    void insert(int val);

    /*返回最小值并删除最小值结点*/
    int deleteMin();
};

MinHeap::MinHeap()
{
    heap = new int[20];
    cur = 0;
}

MinHeap::~MinHeap()
{
    delete[] heap;
}

/*插入值为val的结点*/
void MinHeap::insert(int val)
{
    heap[++cur] = val;
    adjustUp();
}

/*插入结点后，向上调整*/
void MinHeap::adjustUp()
{
    int idx = cur;
    int pIdx = cur / 2;
    while (pIdx > 0 && heap[idx] < heap[pIdx])
    {
        swap(heap[idx], heap[pIdx]);
        idx = pIdx;
        pIdx = pIdx / 2;
    }
}

/*返回最小值并删除最小值结点*/
int MinHeap::deleteMin()
{
    int minVal = heap[1];
    heap[1] = heap[cur--];
    adjustDown(1);
    return minVal;
}

/*删除结点后，向下调整*/
void MinHeap::adjustDown(int idx)
{
    if (idx > cur)
        return;
    int lIdx = idx * 2;
    int rIdx = idx * 2 + 1;

    int minIdx = 0;
    if (lIdx > cur)            //无左右孩子
        return;    
    else if (rIdx > cur)       //只有左孩子
        minIdx = lIdx;
    else minIdx = heap[lIdx] < heap[rIdx] ? lIdx : rIdx;    //左右孩子均非空

    if (heap[idx] > heap[minIdx])
    {
        swap(heap[idx], heap[minIdx]);
        adjustDown(minIdx);
    }
    else return;
}

int main()
{
    int a[] = { 5,1,3,4,2 };
    int len = sizeof(a) / sizeof(a[0]);
    
    /*插入结点构造最小堆*/
    MinHeap* minHeap = new MinHeap();
    for (int i = 0;i < len; i++)
        minHeap->insert(a[i]);

    /*输出堆顶结点的值*/
    for (int i = 0;i < len;i++)
        cout << minHeap->deleteMin() << " ";
    cout << endl;
    
    return 0;
}

结果：

1 2 3 4 5

三、参考

1、http://www.cnblogs.com/vamei/archive/2013/03/20/2966612.html

2、严蔚敏、吴伟民《数据结构》