问题描述:
给定两个单向链表头指针H1,H2,问这俩链表是否相交,如果相交,给出第一次相交的节点。
方案:
分几种情况讨论:
一:H1 H2均为无环链表
这种情况相对比较简单,无环链表相交只能是Y型,也可以理解为T型,如果相交,则它们的最后一个节点必定重复,所以只需判断H1.end() == H2.end()即可。
当判断出确实相交以后,根据H1 H2的长度同时结合快慢指针就可以找到第一次相交的节点,比如H1长度为A,H2长度为B,且A>B,说明H1头结点到所求点的距离比H2头结点到所求点的位置长(A - B),这样用两个指针分别指向H1 H2头结点,叫P1 P2
让P1向后移动(A - B),然后P1 P2同时向后移动,它们相遇的地方就是所求的节点位置。
二:H1 H2只有一个无环链表
这种情况,两个链表绝对不会相交。
三:H1 H2均有环
这种情况就会比较复杂。仍然分两步,第一步判断是否相交,相交也分两种情况:
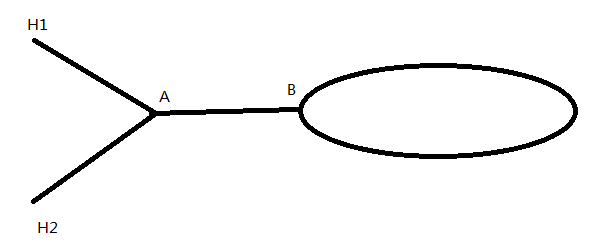
图1
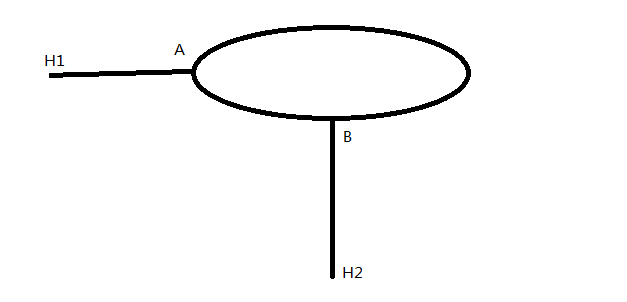
图2
如图所示,如果相交只有这两种情况,图1中,H1 H2他们的环点都在B(环点:本人自定义的一个概念,就是有环单向链表的交叉点),所以如果H1 H2的环点相等,那么二者相交;图二中,二者的环点分别为A B,用一个指针指向A,并一直向后移动,在遇到A之前如果没有遇到B,那么
说明二者不相交,如果遇到B则相交。
下面讨论它们初次相交的节点位置。
仍然是分两种情况,如果是图一,那么方法和两个无环链表一样,首先是计算出二者的长度,然后结合快慢指针就可以找到节点A。
如果是图二,那么不存在初次相交的节点位置。