最长回文串
字符串abcbada最长的回文串为abcba,最长回文串保证首尾字符相同,并且去除首尾后的子串也是回文串,如bcb。
根据这个规律,ab就不是回文串因为首尾不同。abcbada也不是回文串,因为即使首尾相同,其子串bcbad不是回文串,所以abcbada也不是回文串。
动态规划
可以通过动态规划解决字符串的最大回文串的长度问题,其根本思路是依次列举出长度为1~n的回文串,最后返回最大长度n即可。
动态规划的思路在于找出推导公式:
1 首尾元素不同,则不是回文串。
2 首尾元素相同,且去除首尾元素后得子串仍是回文串,则该串为回文串。
假设一个字符串str,我们将上述公式写成伪代码
1 str[begin] != str[end] 则str不是回文串
2 str[begin] == str[end], 且str[begin+1:end-1]是回文串,则str是回文串。
我们用二维数组dp[i][j]表示下标从i到j的字符串是否为回文串,如果是回文串则dp[i][j] == 1,否则dp[i][j] == 0
所以一个回文串应该满足如下条件
dp[i+1][j-1] ==1 && str[i] == str[j]
长度为1时,从i到i的字符串默认为回文串,dp[i][i] = 1
长度为2时,从i到i+1的字符串,判断str[i]==str[i+1] --> dp[i][i+1]=1
长度为3时,从i到i+2的字符串, 判断str[i] == str[i+2] && dp[i+1][i+1] ==1 -> dp[i][i+2] = 1
长度为4时,从i到i+3的字符串,判断str[i] == str[i+3] && dp[i+1][i+2] ==1 -> dp[i][i+3] = 1
.....
推导出dp的规律后开始写代码,将所有可能dp计算出来即可
int max_palindrome(string str, string &palindstr)
{
//初始化二维vector
vector<vector<int>> dp(str.length(), vector<int>(str.length(), 0));
int maxpalind = 0;
//先进行一次遍历统计长度为2和长度为1的dp
//为以后递推长度为n的dp做准备
for (size_t i = 0; i < str.length(); i++)
{
dp[i][i] = 1;
if (i + 1 >= str.length())
{
break;
}
if (str[i] == str[i + 1])
{
dp[i][i + 1] = 1;
maxpalind = 2;
}
}
//"abcdcba"
//外层循环控制长度
for (int len = 3; len <= str.length(); len++)
{
//内层循环控制起始位置
for (int i = 0; i + len - 1 < str.length(); i++)
{
//首尾相同并且去掉首尾后子串仍是回文串
if (str[i] == str[i + len - 1] && dp[i + 1][i + len - 2] == 1)
{
//更新最大长度
maxpalind = len;
//更新dp标记,标记i~i+len-1为回文串
dp[i][i + len - 1] = 1;
palindstr = str.substr(i, i + len - 1);
}
}
}
return maxpalind;
}
依次从长度3计算到字符串长度,最后更新的maxpalind为最大长度,回文串可能不止一个,这里返回最后一个。
在main函数中测试
int main(){
cout << "Dynamic programming ...." << endl;
string str = "abcdcb";
string temp = "";
cout << "str is " << str << endl;
int maxlen = max_palindrome(str, temp);
cout << "max palindrome is " << temp << " size is " << maxlen << endl;
}
程序输出
Dynamic programming ....
str is abcdcb
max palindrome is bcdcb size is 5
中心扩展法
用中心扩展法同样可以解决字符串回文问题,选在每个元素,将其设置为中心,如果满足回文串,则依次向左向右扩充,直到到达边界或者不满足回文串条件为止。
如下图
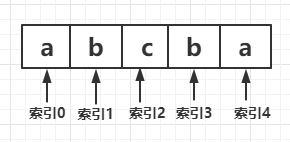
依次从索引为0的节点为中心,直到索引为4的节点,当以某个节点为中心时,判断他的左边节点和右边节点是否相等,如果相等则左节点向左,右节点向右,直到遇到左右节点不相等或者左右节点为边界节点结束。
举例:
当我们找到索引为2的节点c,判断他的左节点为b,右节点也为b,则左节点左移此时指向a,右节点右移指向a,此时左右节点已到达边界,就找到了最大的回文串abcba。
上述思路有一个问题就是面对如下情况,找到的最大回文串是不正确的。
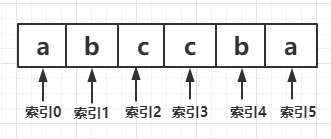
按照上述办法无法找到最大回文串,而此回文串是存在的为abccba, 问题出在偶数节点对称的情况下,我们以索引为2的节点为中心,左节点为b,右节点为c无法找到回文串。解决的方案是将索引2设为左节点,索引3设为右节点就可以找到回文串。
所以扩展的方案修改为上述两种算法的并集
1 以单节点为中心,判断左右节点对称
2 以双节点为中心,判断左右节点对称
先实现根据左右节点相等,则左节点左移,右节点右移的逻辑
int cal_maxlen(string str, int left, int right)
{
while (left >= 0 && right < str.length() && str[left] == str[right])
{
left--;
right++;
}
//因为边界以及左右值不等情况下,此时要-1
// 假设字符串为abcbd 此时left 为0,right 为4=> 4-0-1=3
return right - left - 1;
}
上述代码根据左右节点差值-1计算出回文串长度。
接下来实现以节点为中心遍历展开的逻辑
int center_expend(string str, string &palindstr)
{
int maxpalind = 0;
//从0开始遍历,直到字符串结尾
for (int i = 0; i < str.length() - 1; i++)
{
//以单节点为中心扩展
auto len2 = cal_maxlen(str, i, i);
//以双节点为中心扩展
auto len1 = cal_maxlen(str, i, i + 1);
auto maxlen = 0;
len2 > len1 ? maxlen = len2 : maxlen = len1;
if (maxlen > maxpalind)
{
maxpalind = maxlen;
//此处计算左右节点的位置
//根据总长度maxlen折半找到起始位置
// 假设字符串为abccba, i为2,maxlen为6
//如果字符串为abcba,i为2,maxlen为5,下面规则同样适用
auto start = i - (maxlen - 1) / 2;
auto end = i + maxlen / 2;
palindstr = str.substr(start, end+1);
}
}
return maxpalind;
}
接下来在主函数中做测试
int main(){
cout << "Center expend ...." << endl;
string str2 = "abcddcbams";
string temp2 = "";
int maxlen2 = center_expend(str2, temp2);
cout << "str2 is " << str2 << endl;
cout << "max palindrome is " << temp2 << " size is " << maxlen2 << endl;
}
程序输出
Center expend ....
str2 is abcddcbams
max palindrome is abcddcba size is 8
总结
解决字符串回文的算法还有马拉车算法,就是优先通过遍历在每个字符前后插入'#',再执行中心扩展算法达到o(n)复杂度。这里不做赘述,个人认为善于通过动态规划和中心扩展算法解决回文问题即可。