TensorFlow.NET机器学习入门【4】采用神经网络处理分类问题

 上一篇文章我们介绍了通过神经网络来处理一个非线性回归的问题，这次我们将采用神经网络来处理一个多元分类的问题。

这次我们解决这样一个问题：输入一个人的身高和体重的数据，程序判断出这个人的身材状况，一共三个类别：偏瘦、正常、偏胖。

处理流程如下：

1、收集数据

2、构建神经网络

3、训练网络

4、保存和消费模型

 详细步骤如下：

1、收集数据

对于一个复杂的业务数据，在实际应用时应该是通过收集取得数据，本文的重点不在数据收集，所以我们将制造一批标准数据来进行学习。

关于人体的胖瘦问题，有一个BMI算法，即：BMI=weight / (height * height)，当BMI小于18时，认为偏瘦，当BMI大于28时，认为偏胖，18到28之间，认为正常。

首先随机生成身高和体重的数据，然后计算BMI值，并对结果进行标记，其中，偏瘦标记为0，正常标记为1，偏胖标记为2 。代码如下：

        /// <summary>
        /// 加载训练数据
        /// </summary>
        /// <param name="total_size"></param>    
        private (NDArray, NDArray) PrepareData(int total_size)
        {
            float[,] arrx = new float[total_size, num_features];
            int[] arry = new int[total_size];

            for (int i = 0; i < total_size; i++)
            {
                float weight = (float)random.Next(30, 100) / 100;
                float height = (float)random.Next(140, 190) / 100;
                float bmi = (weight * 100) / (height * height);

                arrx[i, 0] = weight;
                arrx[i, 1] = height;

                switch (bmi)
                {
                    case var x when x < 18.0f:
                        arry[i] = 0;
                        break;

                    case var x when x >= 18.0f && x <= 28.0f:
                        arry[i] = 1;
                        break;

                    case var x when x > 28.0f:
                        arry[i] = 2;
                        break;
                }
            }

2、构建神经网络

相对于简单的非线性模型，本次的网络结构会稍微复杂一些：

       // 网络参数
       int num_features = 2; // data features
       int num_classes = 3; // total output 

        /// <summary>
        /// 构建网络模型
        /// </summary>     
        private Model BuildModel()
        {
            // 网络参数          
            int n_hidden_1 = 64; // 1st layer number of neurons.     
            int n_hidden_2 = 64; // 2nd layer number of neurons.           

            var model = keras.Sequential(new List<ILayer>
            {
                keras.layers.InputLayer(num_features),
                keras.layers.Dense(n_hidden_1, activation:keras.activations.Relu),
                keras.layers.Dense(n_hidden_2, activation:keras.activations.Relu),
                keras.layers.Dense(num_classes, activation:keras.activations.Softmax)
            });

            return model;
        }

首先，本次包含两层神经网络，激活函数均采用RELU，输出层激活函数采用Softmax函数。

和上一篇文章中的网络结构相比看上去复杂很多，但其本质实际上差别不大，只是多了一个Softmax函数。 

请注意观察3个Output节点，如果只是看其中一个节点的话，它实际上就是一个普通的非线性模型。

由于1、2、3三个节点的数据之和不一定等于1，Softmax函数的目的就是要使得最终输出的三个数字之和为1，这样数字本身就可以表示概率了。其计算方法也非常简单：

  

最后我们看一下这个网络的摘要信息：

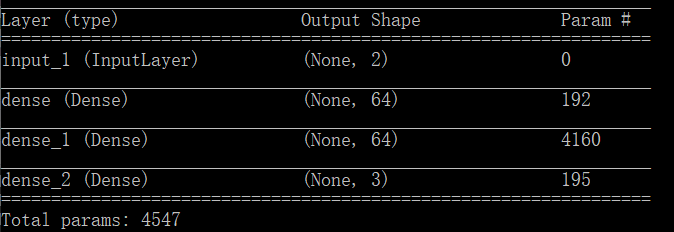
第一层网络的训练参数数量：（2+1）*64=192

第二层网络的训练参数数量：（64+1）*64=4160

输出层网络的训练参数数量：（64+1）*3=195

3、训练网络

            (NDArray train_x, NDArray train_y) = PrepareData(1000);
            model.compile(optimizer: keras.optimizers.Adam(0.001f),
                          loss: keras.losses.SparseCategoricalCrossentropy(),
                          metrics: new[] { "accuracy" });
            model.fit(train_x, train_y, batch_size: 128, epochs: 300);

这里注意一点：损失函数采用稀疏分类交叉熵（SparseCategoricalCrossentropy）方法，对于分类任务，大部分时候都是采用分类交叉熵方法作为损失函数。

下面为二值交叉熵的实现公式：

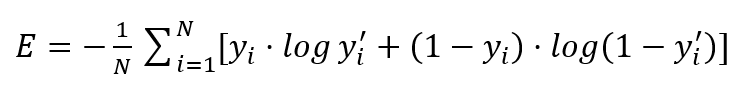
可以不用看公式，简单理解交叉熵的含义：就是如果标记值为1时预测值接近1 或 标记值为0时预测值接近0 则损失函数的值就会比较小。

比如标记值为[1,0,0],预测值为[0.99,0.01,0],则损失比较小，反之，如果预测值为[0.1,0.1,0.8],则损失比较大。

下面时一个二值交叉熵的实现方法：

        private Tensor BinaryCrossentropy(Tensor x, Tensor y)
        {
            var shape = tf.reduce_prod(tf.shape(x));
            var count = tf.cast(shape, TF_DataType.TF_FLOAT);
            x = tf.clip_by_value(x, 1e-6f, 1.0f - 1e-6f);
            var z = y * tf.log(x) + (1 - y) * tf.log(1 - x);
            var result = -1.0f / count * tf.reduce_sum(z);
            return result;
        }

稀疏分类交叉熵和二值交叉熵的区别在于：二值交叉熵需要对标记结果进行独热编码(one-hot)，而稀疏分类交叉熵则不需要。

前面提到，我们对分类结果进行标记，其中，偏瘦标记为0，正常标记为1，偏胖标记为2；而采用二值交叉熵进行计算时，偏瘦标记为[1,0,0]，正常标记为[0,1,0]，偏胖标记为[0,0,1] 。

4、保存和消费模型

训练完成后，我们通过消费这个模型来检查模型的准确性。

        /// <summary>
        /// 消费模型
        /// </summary>      
        private void test(Model model)
        {
            int test_size = 20;
            for (int i = 0; i < test_size; i++)
            {
                float weight = (float)random.Next(40, 90) / 100;
                float height = (float)random.Next(145, 185) / 100;
                float bmi = (weight * 100) / (height * height);

                var test_x = np.array(new float[1, 2] { { weight, height } });
                var pred_y = model.Apply(test_x);

                Console.WriteLine($"{i}:weight={(float)weight} \theight={height} \tBMI={bmi:0.0} \tPred:{pred_y[0].numpy()}");
            }
        }

下面为测试结果：

 

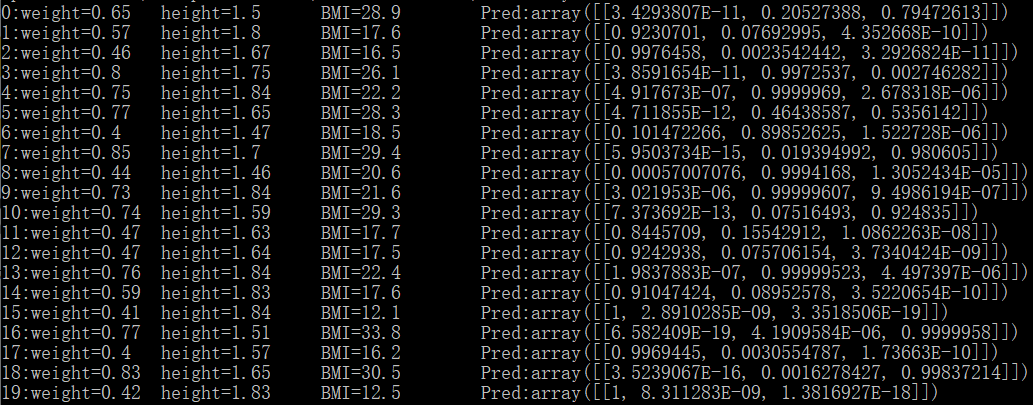
  随便看两条数据：当BMI为30.5时，预测结果为[0,0.0016,0.9983]；当BMI为12.5时，预测结果为：[1,0,0]，可见结果还是准确的。

全部代码如下：

    /// <summary>
    /// 通过神经网络来实现多元分类
    /// </summary>
    public class NN_MultipleClassification_BMI
    {
        private readonly Random random = new Random(1);

        // 网络参数
        int num_features = 2; // data features       
        int num_classes = 3;  // total output .

        public void Run()
        {
            var model = BuildModel();
            model.summary();          

            Console.WriteLine("Press any key to continue...");
            Console.ReadKey();

            (NDArray train_x, NDArray train_y) = PrepareData(1000);
            model.compile(optimizer: keras.optimizers.Adam(0.001f),
              loss: keras.losses.SparseCategoricalCrossentropy(),
              metrics: new[] { "accuracy" });
            model.fit(train_x, train_y, batch_size: 128, epochs: 300);

            test(model);
        }

        /// <summary>
        /// 构建网络模型
        /// </summary>     
        private Model BuildModel()
        {
            // 网络参数          
            int n_hidden_1 = 64; // 1st layer number of neurons.     
            int n_hidden_2 = 64; // 2nd layer number of neurons.           

            var model = keras.Sequential(new List<ILayer>
            {
                keras.layers.InputLayer(num_features),
                keras.layers.Dense(n_hidden_1, activation:keras.activations.Relu),
                keras.layers.Dense(n_hidden_2, activation:keras.activations.Relu),
                keras.layers.Dense(num_classes, activation:keras.activations.Softmax)
            });

            return model;
        }

        /// <summary>
        /// 加载训练数据
        /// </summary>
        /// <param name="total_size"></param>    
        private (NDArray, NDArray) PrepareData(int total_size)
        {
            float[,] arrx = new float[total_size, num_features];
            int[] arry = new int[total_size];

            for (int i = 0; i < total_size; i++)
            {
                float weight = (float)random.Next(30, 100) / 100;
                float height = (float)random.Next(140, 190) / 100;
                float bmi = (weight * 100) / (height * height);

                arrx[i, 0] = weight;
                arrx[i, 1] = height;

                switch (bmi)
                {
                    case var x when x < 18.0f:
                        arry[i] = 0;
                        break;

                    case var x when x >= 18.0f && x <= 28.0f:
                        arry[i] = 1;
                        break;

                    case var x when x > 28.0f:
                        arry[i] = 2;
                        break;
                }
            }

            return (np.array(arrx), np.array(arry));
        }

        /// <summary>
        /// 消费模型
        /// </summary>      
        private void test(Model model)
        {
            int test_size = 20;
            for (int i = 0; i < test_size; i++)
            {
                float weight = (float)random.Next(40, 90) / 100;
                float height = (float)random.Next(145, 185) / 100;
                float bmi = (weight * 100) / (height * height);

                var test_x = np.array(new float[1, 2] { { weight, height } });
                var pred_y = model.Apply(test_x);

                Console.WriteLine($"{i}:weight={(float)weight} \theight={height} \tBMI={bmi:0.0} \tPred:{pred_y[0].numpy()}");
            }
        }
    }

【相关资源】

 源码：Git: https://gitee.com/seabluescn/tf_not.git

项目名称：NN_MultipleClassification_BMI

目录：查看TensorFlow.NET机器学习入门系列目录