TensorFlow.NET机器学习入门【3】采用神经网络实现非线性回归

 上一篇文章我们介绍的线性模型的求解，但有很多模型是非线性的，比如：

 

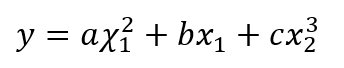
 这里表示有两个输入，一个输出。

现在我们已经不能采用y=ax+b的形式去定义一个函数了，我们只能知道输入变量的数量，但不知道某个变量存在几次方的分量，所以我们采用一个神经网络去定义一个函数。

 

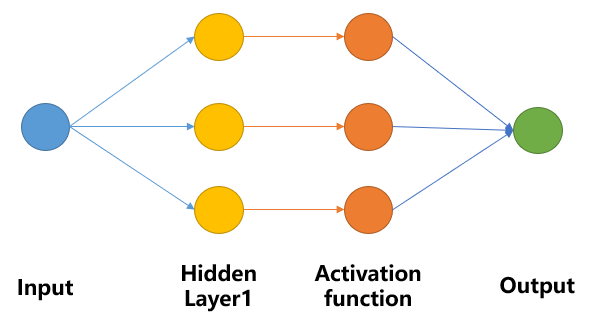
   我们假设只有一个输入、一个输出，神经网络模型结构类似上图，其中蓝色的路径仍为线性模型，红色路径为阶跃函数，是非线性模型。

 以上模型只有三个神经元，设输入为x，隐藏层为h，激活函数输出为a，最终输出为y，整个数据计算流情况如下：

   

  以上共有6+3+1个变量，整个训练的过程就是要解出这些变量。官方教程内有自定义神经网络模型的求解代码，和解线性模型的流程一致，大致以下几个步骤：

1、默认所有k=1，b=0；

2、将x代入模型，求得pred_y，通过pred_y和y计算损失函数，在通过损失函数来计算梯度；

3、通过梯度调整k、b的值

4、重复上述2、3过程，直到损失函数足够小。

具体代码请参看官方示例代码。

我们这篇文章将采用Keras封装好的方法来进行神经网络的训练和应用。

整个程序包括：创建模型、训练模型和应用模型三个过程。

主线程代码：

        public void Run()
        {  
            //1、创建模型
            Model model = BuildModel();  
            model.compile(loss: keras.losses.MeanSquaredError(),
                optimizer: keras.optimizers.SGD(0.02f),
                metrics: new[] { "mae" }); 
            model.summary();       

            //2、训练模型
            (NDArray train_x, NDArray train_y) = PrepareData(1000);
            model.fit(train_x, train_y, batch_size: 64, epochs: 100);

            //3、应用模型（消费）
            test(model);
        }

1、创建模型

BuildModel方法定义如下：

        /// <summary>
        /// 构建网络模型
        /// </summary>     
        private Model BuildModel()
        {
            // 网络参数
            int num_features = 1; // data features 
            int n_hidden_1 = 16; // 1st layer number of neurons.     
            int num_out = 1; // total output .

            var model = keras.Sequential();
            model.add(keras.Input(num_features));
            model.add(keras.layers.Dense(n_hidden_1));
            model.add(keras.layers.LeakyReLU(0.2f));
            model.add(keras.layers.Dense(num_out));

            return model;
        }

以上：Input为输入层，Dense为全连接层，激活函数可选包括：Sigmod、ReLu、LeakyReLu、tanh

model.compile方法定义该模型的训练方式：

loss: keras.losses.MeanSquaredError()表示损失函数采用均方差公式（MSE），这个公式上一篇文章介绍过
optimizer: keras.optimizers.SGD(0.02f)表示参数更新采用随机梯度下降法（SGD），学习率为0.02
metrics: new[] { "mae" }表示要显示的模型评价方法为平均绝对误差(Mean absolute Error)，另外此处还有一个选项为acc，表示准确性( accuracy)，后面在进行分类学习时将采用这种评价方法。

 model.summary()方法将打印出该模型的摘要信息。

 

  

2、训练模型

 (NDArray train_x, NDArray train_y) = PrepareData(1000);

model.fit(train_x, train_y, batch_size: 64, epochs: 100);

首先要加载学习数据，然后将学习数据提供给fit方法进行学习，batch_size 表示每次运算取的数据量，epochs表示循环迭代的次数。所有学习数据用完一次就表示一个epoch，1000除以64等于15.625，所以每计算16次就表示一个epoch。

整个训练过程中将打印出下列信息：

 

  PrepareData方法：

        /// <summary>
        /// 加载训练数据
        /// </summary>
        /// <param name="total_size"></param>    
        private (NDArray, NDArray) PrepareData(int total_size)
        {
            float[,] arrx = new float[total_size, 1];
            float[] arry = new float[total_size];

            for (int i = 0; i < total_size; i++)
            {
                float x = (float)random.Next(-400, 400) / 100;
                float y = x * x;

                arrx[i, 0] = x;
                arry[i] = y;
            }

            NDArray train_X = np.array(arrx);
            NDArray train_Y = np.array(arry);

            return (train_X, train_Y);
        }

该方法生成1000个符合y=x*x的标准数据。

3、应用模型

 学习完成以后，该模型就可以用于实际应用了。我们随机生成一下数据，将模型计算的结果和理论实际的数值进行比较，可以判断模型是否有效。

        /// <summary>
        /// 消费模型
        /// </summary>      
        private void test(Model model)
        {
            int test_size = 10;

            for (int i = 0; i < test_size; i++)
            {
                float x = (float)random.Next(-300, 300) / 100;
                float y = x * x;

                var test_x = np.array(new float[1, 1] { { x } });
                var pred_y = model.Apply(test_x);

                Console.WriteLine($"{i}:x={(float)test_x:0.00}\ty={y:0.0000} Pred:{(float)pred_y[0].numpy():0.0000}");
            }
        }

运行结果如下：

 看结果情况，基本像那么一回事。

【相关资源】

 源码：Git: https://gitee.com/seabluescn/tf_not.git

项目名称：NonlinearRegressionWithKeras

目录：查看TensorFlow.NET机器学习入门系列目录