(1)使用组合数公式利用n!来计算

【程序设计思想】
先将公式化简,上下同时约去(n-k)!
然后计算从(n-k+1)到n的乘积
再用这个乘积除以n!
【流程图】

【源代码】
1 /** 2 * 3 */ 4 package 课堂2; 5 import java.math.BigInteger; 6 import java.util.Scanner; 7 /** 8 * @author 信1605-3 20163471 吴鑫 9 * 10 */ 11 public class LotteryOdds 12 { 13 14 /** 15 * @param args 16 */ 17 public static void main(String[] args) 18 { 19 // TODO 自动生成的方法存根 20 Scanner in = new Scanner(System.in); 21 System.out.print("选择的元素个数:"); 22 int k = in.nextInt(); 23 System.out.print("元素的总个数:"); 24 int n = in.nextInt(); 25 BigInteger bigInteger = BigInteger.valueOf(1l); 26 for (int i = n; i >= n - k + 1; i--) 27 bigInteger = bigInteger.multiply(BigInteger.valueOf(i));////计算(n-k+1)到n的乘积 28 for (int i = 1; i <= k; i++) 29 bigInteger = bigInteger.divide(BigInteger.valueOf(i)); 30 System.out.println("组合数为" + bigInteger.toString()); 31 } 32 33 }
【截图】

(2)使用递推的方法用杨辉三角计算
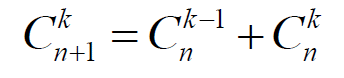
【程序设计思想】
输入n和k的值,创建一个二维数组
通过循环,在第一个循环里,定义i=1,在循环里嵌套循环
定义当j=0时,先判断j是否等于0或者i是否等于j
若成立则输出arr[i-1][j]=1
否则第i-1行j列的数等于第i-2行j列的数与第i-2行j-1列的数之和
最后输出结果。
【流程图】
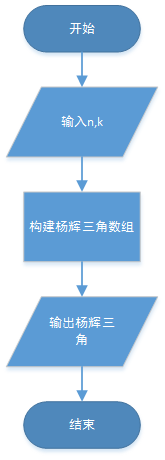
【源代码】
1 package 课堂2; 2 3 import java.util.Scanner; 4 5 /** 6 * @author 信1605-3 20163471 吴鑫 7 * 8 */ 9 10 public class LotteryOdds02 11 { 12 13 public static void main(String[] args) 14 { 15 // TODO 自动生成的方法存根 16 int n, k;// 组合数公式中的n k 17 Scanner input = new Scanner(System.in); 18 System.out.print("选择的元素个数:"); 19 k = input.nextInt(); 20 System.out.print("元素的总个数:"); 21 n = input.nextInt(); 22 int[][] f = new int[27][27];// 构建杨辉三角 23 f[0][0] = 1; 24 for (int i = 1; i <= 24; i++) { 25 for (int j = 1; j <= i + 1; j++) { 26 f[i][j] = f[i - 1][j - 1] + f[i - 1][j]; 27 } 28 } 29 System.out.println("使用递推的方法用杨辉三角形计算结果为 " + f[n + 1][k + 1]);// 输出结果 30 } 31 }
【截图】
(3)利用递归的方法用组合数递推公式计算
【程序设计思想】
类似于杨辉三角的思想
构造一个递归函数用来递归组合数,需要有两个参数。
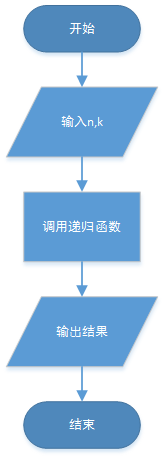
输入n和k
在输出结果中调用递归函数
递归函数中,首先进行数字的判断,考虑特殊情况,
当k=0或n=1或k=n时,输出都为1;
当不是上述情况时,递归计算组合数。
【流程图】
【源代码】
1 /** 2 * 3 */ 4 package 课堂2; 5 6 import java.util.Scanner; 7 8 /** 9 * @author 信1605-3 20163471 吴鑫 10 * 11 */ 12 public class Lotteryodds03 { 13 14 /** 15 * @param args 16 */ 17 public static void main(String[] args) { 18 // TODO 自动生成的方法存根 19 int n, k;// 组合数公式中的n k 20 Scanner input = new Scanner(System.in); 21 System.out.print("选择的元素个数:"); 22 k = input.nextInt(); 23 System.out.print("元素的总个数:"); 24 n = input.nextInt(); 25 System.out.println("使用递归的方法用组合数递推公式计算结果为 "+ recursion(n,k)); 26 } 27 static int recursion(int a,int b) 28 { 29 if(b==0) 30 return 1; 31 else 32 { 33 if(a==1) 34 return 1; 35 else 36 { 37 if(a==b) 38 return 1; 39 else 40 return (recursion(a-1,b-1)+recursion(a-1,b)); 41 } 42 } 43 } 44 }
【截图】


【程序设计思想】
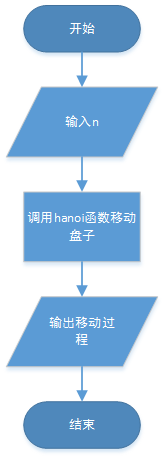
问题可以分为两个操作:一是将n-1个盘从一个座移到另一个座上,这是一个递归的过程,二是将一个盘子从一个座上移到另一个座上。
【流程图】
【源代码】
1 /** 2 * 3 */ 4 package 课堂2; 5 6 import java.util.Scanner; 7 8 /** 9 * @author 信1605-3 20163471 吴鑫 10 * 11 */ 12 public class Hanota { 13 14 /** 15 * @param args 16 */ 17 public static void main(String[] args) { 18 // TODO 自动生成的方法存根 19 int m; 20 System.out.println("请输入要移动的数量:"); 21 Scanner input=new Scanner(System.in); 22 m=input.nextInt(); 23 System.out.println("移动如下:"); 24 hanoi(m,'A','B','C'); 25 } 26 static void hanoi (int n,char one,char two,char three) 27 { 28 if(n==1) move(one,three); 29 else 30 { 31 hanoi(n-1,one,three,two); 32 move(one,three); 33 hanoi(n-1,two,one,three); 34 } 35 } 36 static void move(char x,char y) 37 { 38 System.out.println(x+"-->"+y); 39 } 40 }
【截图】


【程序设计思想】
判读是否回文就是依次判断字符串首尾字符是否一样的过程
声明两个指针i,j,从头开始依次比较首尾字母是否一致
若一致,则是回文,否则不是
【流程图】

【源代码】
1 /** 2 * 3 */ 4 package 课堂2; 5 import java.util.Scanner; 6 /** 7 * @author 信1605-3 20163471 吴鑫 8 * 9 */ 10 public class Palindrome 11 { 12 /** 13 * @param args 14 */ 15 public static void main(String[] args) 16 { 17 // TODO 自动生成的方法存根 18 Scanner input=new Scanner(System.in); 19 String s=input.next();//输入字符串 20 int i,j; 21 i=0;//第一个字符 22 j=s.length()-1;//最后一个字符 23 System.out.println(HuiWen(s,i,j)); 24 } 25 public static boolean HuiWen(String s,int i,int j)//判断字符串是否回文 26 { 27 if(i==j) 28 { 29 return true; 30 } 31 else if((i-1)==j) 32 { 33 return true; 34 } 35 return (s.charAt(i)==s.charAt(j))&&HuiWen(s,i+1,j-1); 36 } 37 }
【截图】