莫队二次离线

P4887 【模板】莫队二次离线（第十四分块(前体)） - 洛谷

给一个序列 (a) ，每次给一个查询区间 ([l,r])

查询 (l le i < j le r) 且 (a_i) 异或 (a_j) 正好有 (k) 个二进制 (bit) 的个数

还是用莫队的思想，在挪的时候更新答案的方式如图

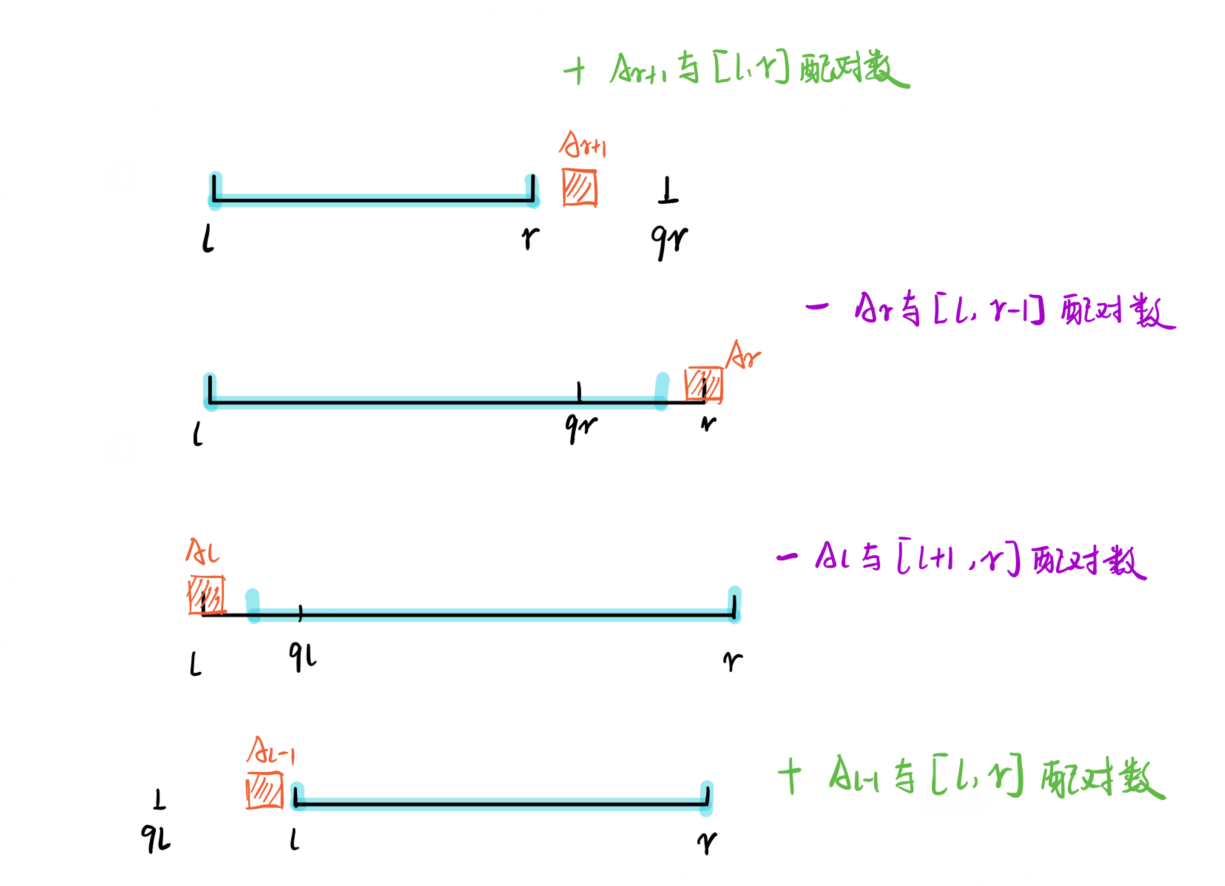
现在我们要解决的问题是如何求 (A_i) 与区间 ([L,R]) 的配对数。

这里我们利用前缀和的思想，令 (S_R) 表示区间 ([1,R]) 与 (A_i) 的配对数

则要求的就是 (S_R - S_{L-1})

两个数配对指的是异或满足题目

我们可以设 (f[i]) 表示 ([1,i]) 与 (A_{i+1}) 的配配对数目所以对于上图的情况有一个(S) 可以用 (f) 来表示，还有一个就再次离线，挂到对应的点上。

求出 (f) 数组

vector<int>nums;
for (int i = 0; i < (1 << 14); i++)
	if (count(i) == k)nums.push_back(i);

for (int i = 1; i <= n; i++) {
	for (int v : nums)g[w[i] ^ v]++;
	f[i] = g[w[i + 1]];
}

举例当 (r < qr) 时

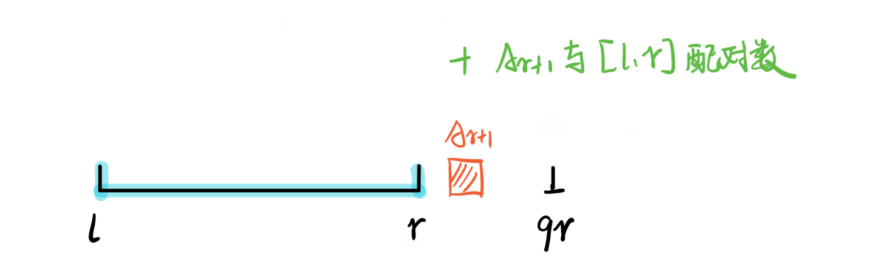
if (r < qr)subs[l - 1].push_back({ i, r + 1, qr, -1 });
while (r < qr) q[i].res += f[r++];

每一次挪动都要加上 (f[r]) 还要减去区间 ([1,l-1]) 与 (A_{r+1},A_{r+2},...,A_{qr}) 的配对数目，对于这个东西，可以把它挂到 (l-1) 上， 这个挂挺形象的。

后面挪 (l) 的时候要注意自己跟自己匹配的情况，只有 (k == 0) 的时候自己可以匹配自己。

注意自己是不能匹配自己的，但是这种情况在计算 (S) 的时候是被计算在内的。

最后处理离线查询

memset(g, 0, sizeof g);
for (int i = 1; i <= n; i++) {
	for (int v : nums)g[v ^ w[i]]++;
	for (auto& x : subs[i]) {
		for (int i = x.l; i <= x.r; i++) {
			q[x.id].res += x.t * g[w[i]];
		}
	}
}

这一块的复杂度是 (r) 的移动次数 (O(n sqrt n)) 量级

/*
 * @Author: zhl
 * @Date: 2020-11-19 20:16:41
 */
#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 1e5 + 10;

int n, m, k, len, ID[N], f[N], g[N], w[N];
ll ans[N];
struct Query {
	int id, l, r;
	ll res;
	bool operator < (const Query& b)const {
		if (ID[l] != ID[b.l]) return ID[l] < ID[b.l];
		return r < b.r;
	}
}q[N];

struct subquery {
	int id, l, r, t;
};
vector<subquery>subs[N];

int count(int n) {
	int ans = 0;
	while (n) ans++, n -= -n & n;
	return ans;
}
int main() {
	scanf("%d%d%d", &n, &m, &k);
	for (int i = 1; i <= n; i++)scanf("%d", w + i);

	len = sqrt(n);
	for (int i = 1; i <= n; i++)ID[i] = i / len;

	vector<int>nums;
	for (int i = 0; i < (1 << 14); i++)if (count(i) == k)nums.push_back(i);

	for (int i = 1; i <= n; i++) {
		for (int v : nums)g[w[i] ^ v]++;
		f[i] = g[w[i + 1]];
	}

	for (int i = 1; i <= m; i++) {
		scanf("%d%d", &q[i].l, &q[i].r); q[i].id = i;
	}

	sort(q + 1, q + 1 + m);

	int l = 1, r = 0;
	for (int i = 1; i <= m; i++) {
		int ql = q[i].l, qr = q[i].r;
		//在 l - 1 处 挂上一个离线查询
		if (r < qr)subs[l - 1].push_back({ i, r + 1, qr, -1 });
		while (r < qr) q[i].res += f[r++];

		if (r > qr)subs[l - 1].push_back({ i, qr + 1,r ,1 });
		while (r > qr) q[i].res -= f[--r];

		if (l < ql)subs[r].push_back({ i, l, ql - 1, -1 });
		while (l < ql) q[i].res += f[l - 1] + !k, l++;

		if (l > ql)subs[r].push_back({ i, ql, l - 1,1 });
		while (l > ql) q[i].res -= f[l - 2] + !k, l--;
	}
	memset(g, 0, sizeof g);
	for (int i = 1; i <= n; i++) {
		for (int v : nums)g[v ^ w[i]]++;
		for (auto& x : subs[i]) {
			for (int i = x.l; i <= x.r; i++) {
				q[x.id].res += x.t * g[w[i]];
			}
		}
	}
	for (int i = 2; i <= m; i++) q[i].res += q[i - 1].res;
	for (int i = 1; i <= m; i++)ans[q[i].id] = q[i].res;
	for (int i = 1; i <= m; i++)printf("%lld
", ans[i]);
}