文艺平衡树Splay

Splay 是平衡树

(Splay) 是平衡树的一种

基本思想是， 对于查找频率较高的节点，使其处于离根节点相对较近的节点。

Spaly的基本操作有

• rotate（旋转）
• splay （伸展）
• push_up
• push_down

struct Node {
	int son[2], fa, val;
	int size, flag;

	void init(int _val, int _fa) {
		val = _val; fa = _fa;
		size = 1;
	}
}tr[N];

rotate()

这个旋转操作跟数据结构里学的平衡树旋转操作是一样的。

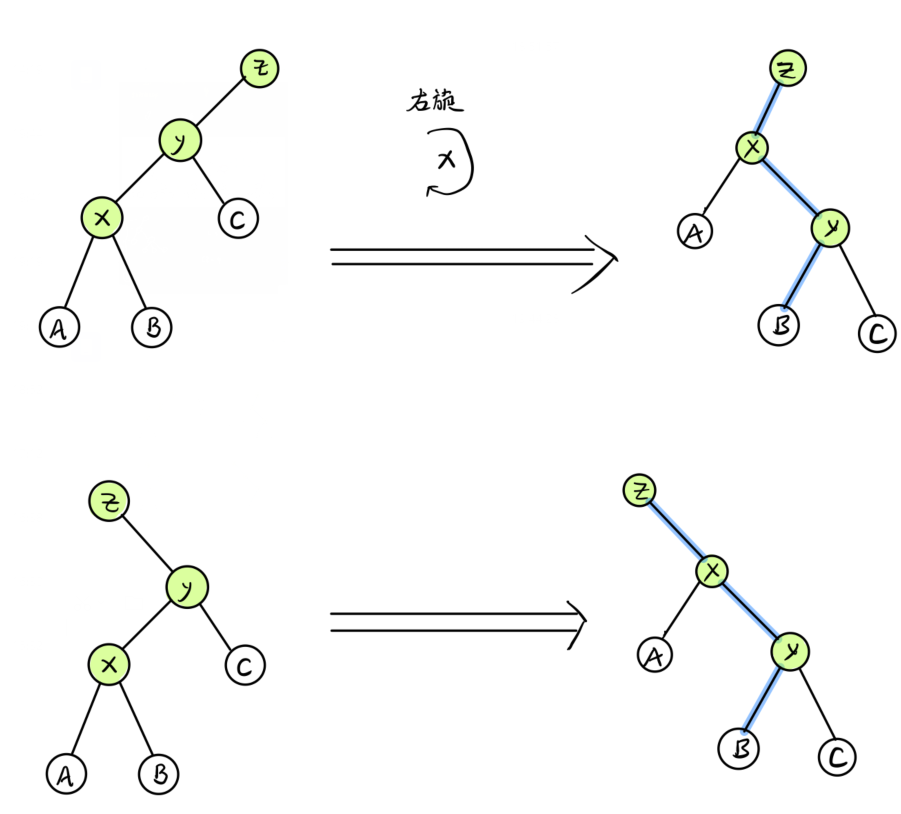
如下图，画的是右旋 (x) 的操作，蓝色的边表示信息发生了改变

void rotate(int x) {
	int y = tr[x].fa, z = tr[y].fa;
	int k = (tr[y].son[1] == x); // k = 0 表示 x 是 y 的左儿子
	tr[z].son[tr[z].son[1] == y] = x, tr[x].fa = z;
	tr[y].son[k] = tr[x].son[k ^ 1], tr[tr[x].son[k ^ 1]].fa = y;
	tr[x].son[k ^ 1] = y, tr[y].fa = x;
	push_up(y), push_up(x);
}

代码中修改信息的三行对应了三条蓝边，上图表示的情况是 (k=0)

splay()

接口 splay(int x,int k) 把节点 (u) 转到 (k) 下面，若 (k) 为 (0) , 则转到根的位置

void splay(int x, int k) {
	while (tr[x].fa != k) {
		int y = tr[x].fa, z = tr[y].fa;
		if (z != k) {
			if ((tr[y].son[1] == x) ^ (tr[z].son[1] == y))rotate(x);
			else rotate(y); //转y才是log复杂度
		}
		rotate(x);
	}
	if (!k)root = x;
}

if ((tr[y].son[1] == x) ^ (tr[z].son[1] == y)) 表示的是不是链状，此时转两下 (x) ,若是链状，则需要先转一下 (y) 再转 (x) ，不能转两次 (x)

push_up()

类似线段树的 push_up() ，一般只需要维护 (size)

void push_up(int u) {
	tr[u].size = tr[tr[u].son[0]].size + tr[tr[u].son[1]].size + 1;
}

push_down()

在需要 (lazytag) 时将标记下传