Global Round 10

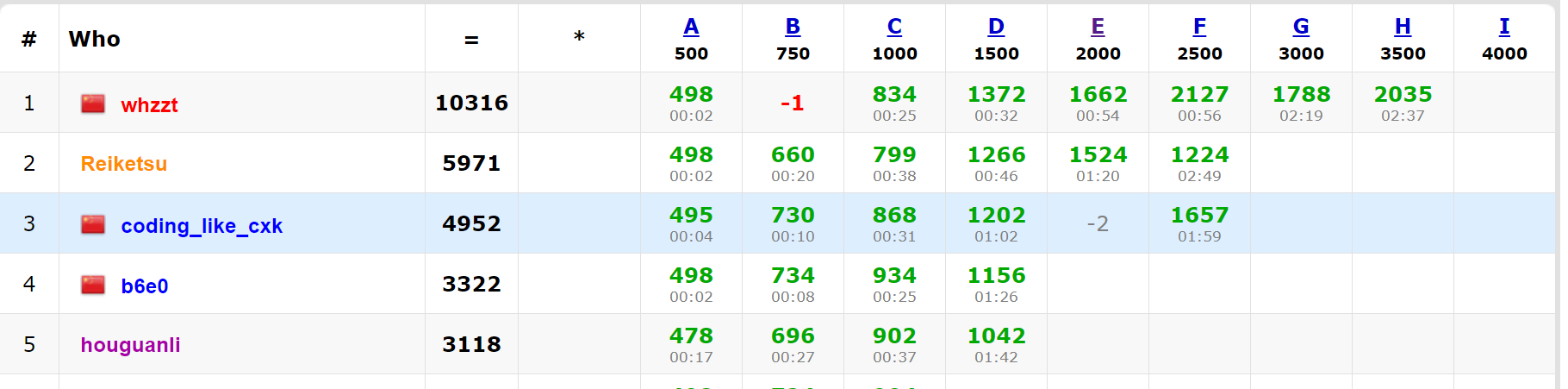
还不错，就是这个交互题简直毒瘤，我现在都不知道为什么过了1k+

F题其实挺简单的，过的人有点少了。

还是嫖到了155分，还不错。

room里面有好多大佬，太恐怖了。

官方题解

A. Omkar and Password

题意

给一个数组，每次可以选择数值不同的相邻项，合并它们（删除这两个项，把他们的和插到原来的位置），问若干次操作后数组的最小长度

思路：

只要不是全一样的数，最后都可以操作成一个数

	cin >> T;
    while(T--){
        cin >> n;
        set<int>s;
        for(int i = 1;i <= n;i++){
            cin >> A[i];
            s.insert(A[i]);
        }
        if(s.size() > 1){
            cout << 1 << endl;
        }
        else{
            cout << n << endl;
        }
    }

B. Omkar and Infinity Clock

题意：

给数组 (A) , 问经过 (k) 次操作后 (A) 的模样。 每次操作中， (d = max(A)) , $A_i = d - A_i , i in [1,n] $

思路:

最开始 (A) 中可能有负数，操作一次后，就没有了。然后就开始循环了。

	cin >> T;
    while(T--){
        cin >> n >> k;
        
        for(int i = 1;i <= n;i++){
            cin >> A[i];
        }
        int Mx = *max_element(A+1,A+1+n);
        for(int i = 1;i <= n;i++){
            A[i] = Mx - A[i];
        }

        if(k % 2 == 0){
            Mx = *max_element(A+1,A+1+n);
            for(int i = 1;i <= n;i++){
                A[i] = Mx - A[i];
            }
        }

        for(int i = 1; i<= n;i++){
            printf("%d%s",A[i],i == n ? "
" : " ");
        }

    }

C. Omkar and Waterslide

题意：

给一个数组 (A) ,每次可以选取一个非降序列，使得序列中每个值增加一。问最少操作多少次使得整个数组 非降

思路：

(A) 肯定由若干个降序序列构成，对于一个降序序列，操作次数为最大值减去最小值，若当前降序序列的最大值小于前一个降序序列的最大值，其实不需要额外的花费。

	cin >> T;
	while (T--) {
		cin >> n;

		for (int i = 1; i <= n; i++) {
			cin >> A[i];
		}

		int idx = 1;
		int ans = 0;
		while (idx <= n) {
			int Max = A[idx];
			int Min = A[idx];
			while (idx + 1 <= n && A[idx] > A[idx + 1]) {
				Max = max(Max, A[idx+1]);
				Min = min(Min, A[idx+1]);
				idx++;
			}
			ans += Max - Min;

			idx++;
		}
		cout << ans << endl;
	}

D. Omkar and Bed Wars

题意：

(1) 到 (n) 围成一个圈，(1) 在 (n) 的右边。

每个人可以选择攻击左边的人，或者攻击右边的人。

给定一个 L R 序列，问是否满足规则

• 如果只被一个人攻击，则他应该攻击这个人
• 如果被两个人攻击或者没有人攻击，则可以随意攻击

可以把 L 改成 R，R 改成 L

问最少需要修改几次使得序列合法

思路：

自己多画图模拟一下，肯定是由若干个 L 和 若干个 R 序列构成的，

最优的策略是三个抱团，LLR 或者 LRR 这样

	cin >> T;
    while(T--){
        cin >> n;
        
        string s;
        cin >> s;
        vector<int>L;

        for(int i = 0;i < s.size();i++){
            int cnt = 1;
            while(i + 1 < s.size() && s[i] == s[i+1]){
                i++;
                cnt++;
            }
            L.push_back(cnt);
        }
        if(s[s.size() - 1] == s[0] && L.size() > 1){
            L[0] += L[L.size()-1];
            L.pop_back();
        }
        if(L.size() == 1){
            if(L[0] <= 2){
                cout << 0 << endl;
            }
            else{
                cout << (L[0] + 2) / 3 << endl;
            }
        }
        else{
            int ans = 0;
            for(int i : L){
                ans += i/3;
            }
            cout << ans << endl;
        }
    }

E. Omkar and Duck

待补

F. Omkar and Landslide

题意:

模拟一个山体滑坡，给一个升序序列(H) ，代表了山的高度，每个时刻，若 (h_j + 2 leq h_{j + 1}) ,则 (h_{j+1}) 减少一， (h_i) 增加一，问最后 (H) 的样子

思路：

其实多画图琢磨之后这道题挺简单的。它是由一个初始差为 (1) 的等差数列，然后由前往后依次增一

	scanf("%d", &n);

	long long sum = 0;
	for (int i = 1; i <= n; i++) {
		scanf("%lld", A + i);
	}
	for (int i = 1; i <= n; i++) {
		sum += (A[i] - A[1] - i + 1);
	}
	long long base = A[1];
	for (int i = 1; i <= n; i++) {
		A[i] = base + i - 1 + sum / n;
	}
	for (int i = 1; i <= sum % n; i++) {
		A[i]++;
	}
	for (int i = 1; i <= n; i++) {
		printf("%lld%s", A[i], i == n ? "
" : " ");
	}